Writing in Environmental Science & Technology (May 1986), Joseph Fiksel researched the problem of compensating victims of chronic diseases (such as cancer and birth defects) who are exposed to hazardous and toxic substances. The key to compensation, as far as the U.S. judicial system is concerned, is the probability of causation (i.e., the likelihood, for a person developing the disease, that the cause is due to exposure to the hazardous substance). Usually, the probability of causation must be greater than .50 for the court to award compensation. Fiksel gave examples of how to calculate the probability of causation for several different scenarios.†
a. ”Ordinary causation,” as defined by Fiksel, “describes a situation in which the presence of a single factor, such as asbestos insulation, is believed to cause an effect, such as mesothelioma.” For this situation, define the following events:
D: {Effect (disease) occurs}
A: {Factor A present}
Under ordinary causation, if A occurs, then D must occur. However, D can also occur when factor A is not present. The probability of causation for factor A, then, is the conditional probability P (A | D). Show that the probability of causation for factor A is

where P_o is the probability that the effect occurs when factor A is not present, and P₁ is the probability that the effect occurs when factor A is either present or not. (Note: To epidemiologists, P₁ is often called the overall risk rate for the disease and P₁ - P_o is the additional risk attributable to the presence of factor A.) (Hint: The simple events for this experiment are {D^c ∩ A^C, D ∩ A, and D ∩ A^c) . Write P_o and P₁ in terms of the simple events.)
b. Fiksel defined simultaneous exclusive causation as “a situation in which two or more causal factors are present but the resulting effect is caused by one and only one of these factors.” Consider two factors, A and B, and let B be the event that factor B is present. In this situation, if either A or B occurs, then D must occur. However, both A and B cannot occur simultaneously (i.e., A and B are mutually exclusive). Assuming that D cannot occur when neither A nor B occurs, show that the probabilities of causation for factors A and B are, respectively,

where P₁ is the probability that the effect occurs when factor A is present and P₂ is the probability that the effect occurs when factor B is present. (Hint: The simple events for this experiment are D ∩ A ∩ B^c, D ∩ A^c ∩ B} 

c. Simultaneous joint causation, wrote Fiksel, describes a more realistic situation “in which several factors can contribute in varying degrees to the occurrence of an effect. For example, a cigarette smoker who is exposed to radiation and chemical carcinogens in the  workplace may develop a lung tumor. Whether the  tumor was caused wholly by one factor or by a combination of factors is, at present, impossible to determine.” For this case, consider two factors, A and B,
which affect D independently. Also, assume that if either
A or B, or both occur, then D must occur; D cannot occur if neither A nor B occurs. Show that the probabilities of causation for factors A and B are, respectively,

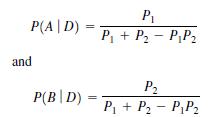
where P₁ is the probability that the effect occurs when factor A is present and P₂ is the probability that the effect occurs when factor B is present. (Hint: The simple events for this experiment are {D^c ∩ A^c ∩ B^c, D ∩ A ∩ B^c, D ∩ A^c ∩ B and D ∩ A ∩ B}. )

Transcribed Image Text:

P, - Po P(A |D) P1