Consider the gear-train system shown in Figure 5.100. The system consists of a rotational cylinder and a pair of gears. The gear ratio is \(N=r_{1} / r_{2}\). The applied torque on the cylinder is \(\tau_{\mathrm{a}}\). Assume that the gears are connected with flexible shafts, which can be approximated as two torsional springs of stiffness, \(K_{1}\) and \(K_{2}\), respectively.

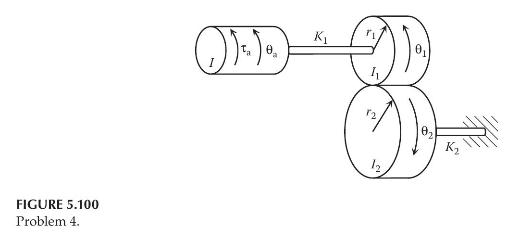
a. Draw the necessary free-body diagrams, and derive the differential equations of motion.

b. Using the differential equations obtained in Part (a), determine the state-space representation. Use \(\theta_{a}, \theta_{1}, \omega_{a}\) and \(\omega_{1}\) as the state variables, and use \(\theta_{2}\) and \(\omega_{2}\) as the output variables.

Transcribed Image Text:

FIGURE 5.100 Problem 4. Ta K