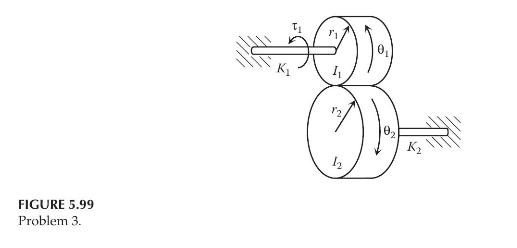
Consider the one-degree-of-freedom system shown in Figure 5.99. The system consists of two gears of mass moments of inertia \(I_{1}\) and \(I_{2}\) and radii \(r_{1}\) and \(r_{2}\), respectively. The applied torque on gear 1 is \(\tau_{1}\). Assume that the gears are connected with flexible shafts, which can be approximated as two torsional springs of stiffness, \(K_{1}\) and \(K_{2}\), respectively.

a. Draw the necessary free-body diagrams, and derive the differential equation of motion in \(\theta_{1}\).

b. Using the differential equation obtained in Part (a), determine the transfer function \(\Theta_{2}(s) / T_{1}(s)\).

c. Using the differential equation obtained in Part (a), determine the state-space representation with \(\theta_{2}\) as the output.

Transcribed Image Text:

FIGURE 5.99 Problem 3. 12 O 12