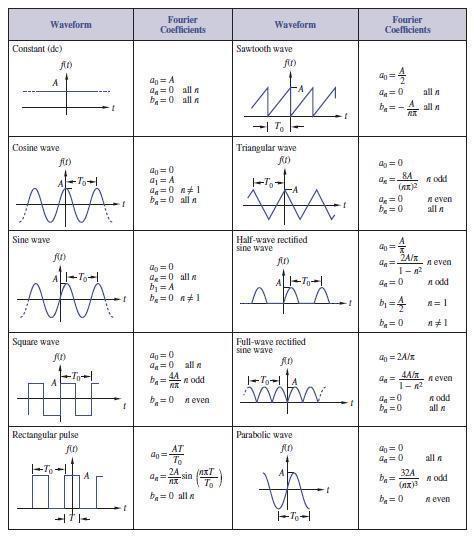
Question: In the rectangular-pulse waveform shown in Figure 134, the width of the pulse is one-third the period, T =T0=3. The waveform is to pass through
In the rectangular-pulse waveform shown in Figure 13–4, the width of the pulse is one-third the period, T =T0=3. The waveform is to pass through a low-pass filter and then through a resistive load. The load must receive at least 97% of the average power in the original waveform.
Determine the minimum value of N such that if the filter passes components V0,V1,V2,…,VN, the load will receive the required amount of power.
(Hint: You may want to use MATLAB to perform the calculations.)
Waveform Constant (dc) A Cosine wave fit) -To- Fourier Coefficients 4 = A a=0 all n b=0 all a=0 a = A 4 01 b=0 all n Waveform Fourier Coefficients Sawtooth wave fir) %=0 all n b=- all n To Triangular wave Kt) 9=0 -To- a = 84 nodd -A (x) %=0 b=0 even To- Sine wave f(r) AL-To- AM Square wave A K(1) a=0 =0 all b = A b=0n1 4 =0 Half-wave rectified sine wave a = fit) A-T- 2A/x vn 1-2 =0 odd b = =1 b=0 1 Full-wave rectified sine wave 4-0 all n %=2A/x b = nodd 4A/x 1-2 neven b=0 neven %=0 b=0 odd Rectangular pulse fin To A a=2sin(x) b=0 all a Parabolic wave AT %=0 Q=0 all n 32A b = nodd (x3 b=0 neven
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


