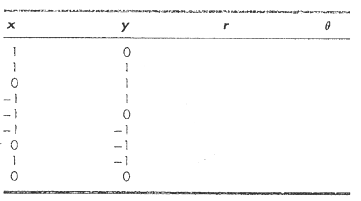
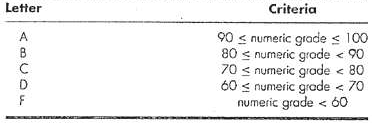
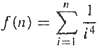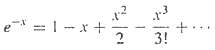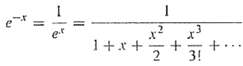Numerical Methods For Engineers 5th Edition Steven C. Chapra, Raymond P. Canale - Solutions
Unlock the full potential of your studies with our comprehensive solutions to "Numerical Methods For Engineers 5th Edition" by Steven C. Chapra and Raymond P. Canale. Access a wide array of step-by-step answers and solved problems designed to enhance your understanding. Whether you're looking for a solution manual, answers key, or chapter solutions, our resources are here to provide clarity. Benefit from the instructor manual and test bank to excel in your coursework. Discover the convenience of online solutions and free downloadable PDFs, tailored to assist you in mastering the textbook's concepts effectively.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


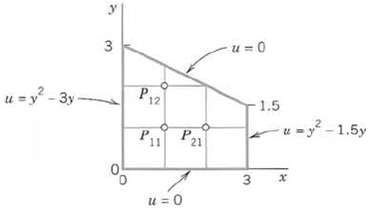
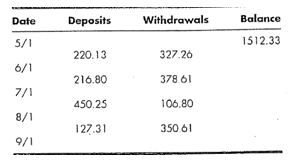

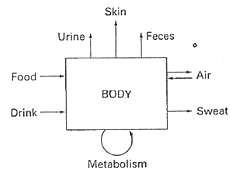
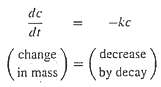
.png)
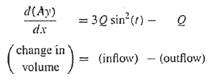
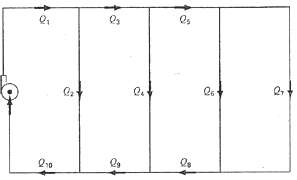
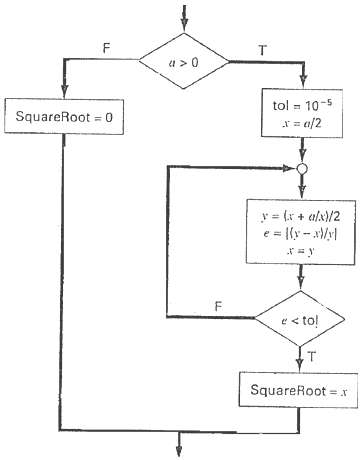
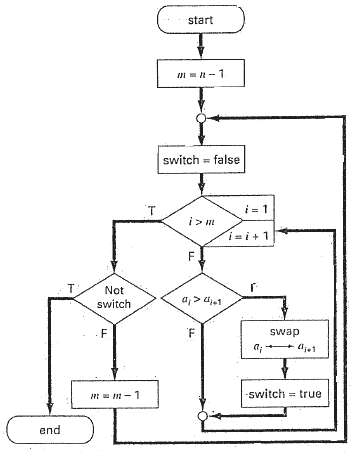
-1.png)
-2.png)