Show that in the integral domain of Exercise 3 every element can be factored into a product of irreducible, but this factorization need not be unique (in the sense of Definition 3.5 (ii)).

In Exercise 3

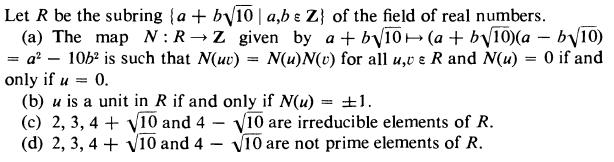
Data from definition 3.5

An integral domain Risa unique factorization domain provided that:

(i) every nonzero non unit element a of R can be written a = C₁C₂ • · • C_n, with C₁, ••• , C_n irreducible.

(ii) I∫ a= C₁C₂· · ·C_n and a= d₁d₂· · ·d_m (c_i,d_i irreducible), then n = m and for some permutation σ o∫ {1, 2,..., n},c_i and d_σ(i) for associates for every i.