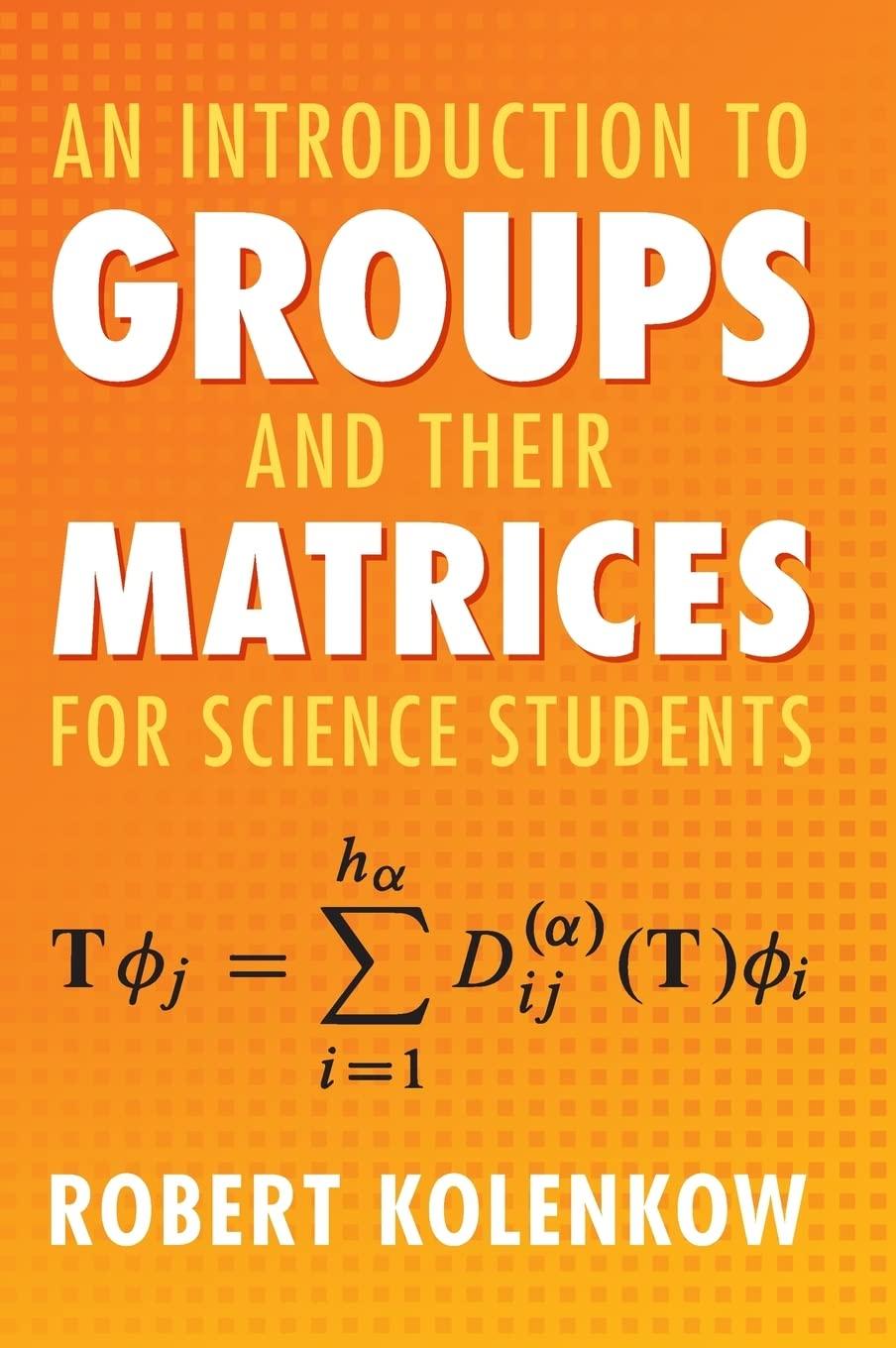As in Problem 9, consider a planar system of three identical masses and three identical springs. At equilibrium each mass is at the apex of an equilateral triangle. A spring links each pair of masses.

The reducible representation based on coordinate displacements can be expressed as the sum of irreducible representations from the character table in Problem 9 as \(A_{1}+A_{2}+B_{2}+2 E_{1}+E_{2}\).

(a) Express the reducible representation of the nontrivial normal modes as a sum of irreducible representations using the character table from Problem 9.

(b) How many different nontrivial frequencies are exhibited by the system's normal modes?

Data from Problem 9

Consider a planar system of three identical masses and three identical springs. At equilibrium each mass is at the apex of an equilateral triangle. A spring links each pair of masses.

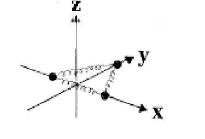
Here is its character table (inversions omitted).

Use coordinate displacements as the basis for a reducible representation. In this representation what are the characters of each of the symmetry operations listed in the table?

Transcribed Image Text:

+4 y