In Example 1, change 2cos to tan. Data from Example 1 Solve the equation 2 cos
Question:
In Example 1, change 2cosθ to tanθ.
Data from Example 1
Solve the equation 2 cosθ − 1 = 0 for all values of θ such that 0 ≤ θ ≤ 2π. Solving the equation for cosθ, we obtain cosθ = 1/2. The problem asks for all values of θ from 0 to 2π that satisfy the equation. We know that the cosines of angles in the first and fourth quadrants are positive. Also, we know that cos π/3 = 1/2 which means that π/3 is the reference angle. Therefore, the solution proceeds as follows:
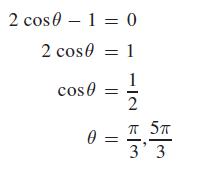
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Basic Technical Mathematics
ISBN: 9780137529896
12th Edition
Authors: Allyn J. Washington, Richard Evans
Question Posted:





