A thermal power station discharges its cooling water into a river. An environmental scientist wants to determine if this has adversely a ected the dissolved oxygen level. She takes samples of water one kilometer upstream from the power station, and one kilometer downstream from the power station, and measures the dissolved oxygen level. The data are:

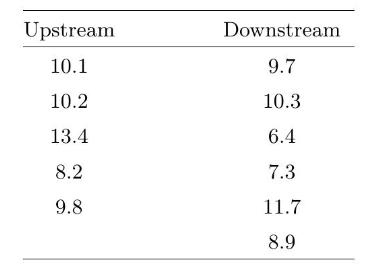
(a) We will assume that the observations come from \(\operatorname{normal}\left({ }_{1}{ }^{2}\right)\) and normal \(\left(2^{2}\right.\) ), where \({ }^{2}=2^{2}\). Use independent normal ( \(\left.m s^{2}\right)\) prior distributions for 1 and 2 , respectively, where \(m=10\) and \(s^{2}=2^{2}\). Find the posterior distributions of 1 and \({ }_{2}\), respectively.
(b) Find the posterior distribution of 12.
(c) Find a \(95 \%\) Bayesian credible interval for \(1 \quad 2\).
(d) Perform a Bayesian test of the hypothesis
\[
\begin{array}{lllllll}
H_{0}: & 1 & 2 & 0 & \text { versus } & H_{1}: & 1
\end{array}>0
\]
at the \(5 \%\) level of signi cance. What conclusion can we draw?

Transcribed Image Text:

Upstream Downstream 10.1 9.7 10.2 10.3 13.4 6.4 8.2 7.3 9.8 11.7 8.9