Efficacy of an HIV vaccine. New, effective AIDS vaccines have been developed through the process of “sieving”—that is, sifting out infections with some strains of HIV. Consider a vaccine designed to eliminate a particular strain of the virus.

To test the efficacy of the vaccine, a clinical trial was conducted.

The trial consisted of 7 AIDS patients vaccinated with the new drug and 31 AIDS patients who were treated with a placebo (no vaccination). Of the 7 vaccinated patients, 2 tested positive and 5 tested negative at the end of a follow-

up period. Of the 31 unvaccinated patients, 22 tested positive and 9 tested negative. (These data are saved in the HIVVAC1 file.)

a. Construct a contingency table for the data. Then, conduct a test to determine whether the vaccine is effective in treating this strain of HIV. Use a = .05.

b. Are the assumptions for the test you carried out in part a satisfied? What are the consequences if the assumptions are violated?

c. In the case of a 2 * 2 contingency table, R. A. Fisher

(1935) developed a procedure for computing the exact p-value for the test (called Fisher’s exact test). The method utilizes the hypergeometric probability distribution of Chapter 4 (p. 248). Consider the hypergeometric probability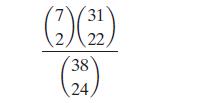

which represents the probability that 2 out of 7 vaccinated AIDS patients test positive and 22 out of 31 unvaccinated patients test positive—that is, the probability of the result of the clinical trial, given that the null hypothesis of independence is true. Compute this probability (called the probability of the contingency table).

d. Refer to part

c. Now consider two other possible results from the clinical trial that are different from the original results. Result 2: Only 1 of the 7 vaccinated patients tests positive; 23 of the 31 unvaccinated patients test positive. Result 3: None of the 7 vaccinated patients tests positive; 24 of the 31 unvaccinated patients test positive. Create two contingency tables, one for each of these results. (These data are saved in the HIVVAC2 and HIVVAC3 files respectively.) Note that these two contingency tables have the same marginal totals as the original table in part

a. Explain why each of these tables provides more evidence to reject the null hypothesis of independence than does the original table. Then, compute the probability of each table, using the hypergeometric formula.

e. The p-value of Fisher’s exact test is the probability of observing a result at least as unsupportive of the null hypothesis as is the observed contingency table, given the same marginal totals. Sum the probabilities of parts c and d to obtain the p-value of Fisher’s exact test.
(To verify your calculations, check the p-value labeled Left-sided Pr * F at the bottom of the SAS printout shown below.) Interpret this value in the context of the vaccine trial.

Transcribed Image Text:

31 (2)(3) 38 24 22