Let a n be a series with positive terms and let r n = a n+1 /a
Question:
Let Σan be a series with positive terms and let rn = an+1/an . Suppose that limn→∞ rn = L < 1, so Σan converges by the Ratio Test. As usual, we let Rn be the remainder after n terms, that is,
Rn = an+1 + an+2 + an+3 + ∙ ∙ ∙
(a) If {rn} is a decreasing sequence and rn+1< 1, show, by summing a geometric series, that
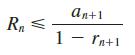
(b) If {rn} is an increasing sequence, show that
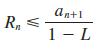
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus Early Transcendentals
ISBN: 9781337613927
9th Edition
Authors: James Stewart, Daniel K. Clegg, Saleem Watson, Lothar Redlin
Question Posted:





