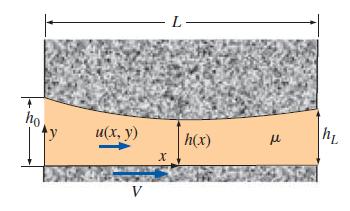
Consider the slipper-pad bearing of Fig. P1027. The drawing is not to scale; in actuality, h
Question:
Consider the slipper-pad bearing of Fig. P10–27. The drawing is not to scale; in actuality, h ≪ L. This case differs from that of Prob. 10–23 in that h(x) is not linear; rather h is some known, arbitrary function of x. Write an expression for axial velocity component u as a function of y, h, dP/dx, V, and μ. Discuss any differences between this result and that of Prob. 10–26.
FIGURE P10–27
Data from Problem 26
Consider again the slipper-pad bearing of Prob. 10–23.
List appropriate boundary conditions on u.
Solve the creeping flow approximation of the x-momentum equation to obtain an expression for u as a function of y (and indirectly as a function of x through h and dP/dx, which are functions of x). You may assume that P is not a function of y. Your final expression should be written as u(x, y) 5 f (y, h, dP/dx, V, and μ). Name the two distinct components of the velocity profile in your result.
Nondimensionalize your expression for u using these appropriate scales:
![]()
Data from Problem 23
A slipper-pad bearing (Fig. P10–23) is often encountered in lubrication problems. Oil flows between two blocks; the upper one is stationary, and the lower one is moving in this case. The drawing is not to scale; in actuality, h ≪ L. The thin gap between the blocks converges with increasing x. Specifically, gap height h decreases linearly from h0 at x = 0 to hL at x = L. Typically, the gap height length scale h0 is much smaller than the axial length scale L. This problem is more complicated than simple Couette flow between parallel plates because of the changing gap height. In particular, axial velocity component u is a function of both x and y, and pressure P varies nonlinearly from P = P0 at x = 0 to P = PL at x = L. (∂P/∂x is not constant). Gravity forces are negligible in this flow field, which we approximate as two-dimensional, steady, and laminar. In fact, since h is so small and oil is so viscous, the creeping flow approximations are used in the analysis of such lubrication problems. Let the characteristic length scale associated with x be L, and let that associated with y be h0 (x ∼ L and y ∼ h0). Let u ∼ V. Assuming creeping flow, generate a characteristic scale for pressure difference ΔP = P – P0 in terms of L, h0, μ, and V.
FIGURE P10–23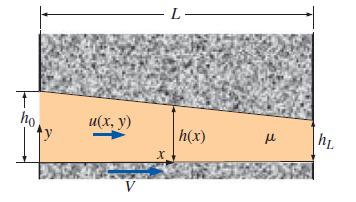
Step by Step Answer:

Fluid Mechanics Fundamentals And Applications
ISBN: 9780073380322
3rd Edition
Authors: Yunus Cengel, John Cimbala





