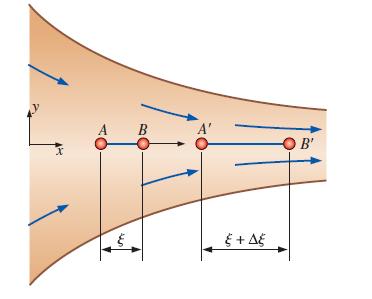
Using the results from Prob. 4–52 and the fundamental definition of linear strain rate (the rate of increase in length per unit length), develop an expression for the linear strain rate in the x-direction (ε_xx) of fluid particles located on the centerline of the channel. Compare your result to the general expression for ε_xx in terms of the velocity field, i.e., ε_xx = ∂u/∂x.

Data from Problem 4-52.

Converging duct flow is modeled by the steady, two-dimensional velocity field of Prob. 4–17. Since the flow is symmetric about the x-axis, line segment AB along the x-axis remains on the axis, but stretches from length ξ to length + 1 Δξ as it flows along the channel centerline (Fig. P4–52). Generate an analytical expression for the change in length of the line segment, Δξ.

Transcribed Image Text:

A Un B A' { + Δέ Ο Β'