Using the Heisenberg equation of motion Eq. (4.30) and the Hamiltonian of a free particle in a magnetic field given by Eq. (4.171), evaluate the velocity operators vx, vy, and vz. Note how the magnetic field has modified one of the velocities. How does the presence of an electric field, if at all, modify the velocity operators? As a consequence of relativity, the spin magnetic moment of an electron is coupled to its own orbit via the interaction:

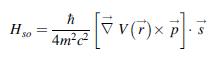where V(r^→) is the total potential seen by the electron and s^→ is the spin operator. What is the effect of the spin-orbit interaction on the quantum mechanical definition of the velocity operator (use the Heisenberg equation of motion Eq. (4.30)). What is the dependence of the spin-orbit coupling on the orbital angular momentum L, if V(r^→)is the Coulomb potential of the hydrogen atom?

Transcribed Image Text:

V(7) H so 4m?c2