Suppose that a long and shallow cavity of length L and depth H is filled with liquid, as in Fig. P7.12. If something at the top surface causes the liquid there to move from left to right (i.e., if v_x > 0 at y = H), a circulating flow is created, as indicated by the arrows. However, if L⁄H is large enough, the flow in the central region will be fully developed. This problem focuses on that region, centered on x = 0, where v_x = v_x(y).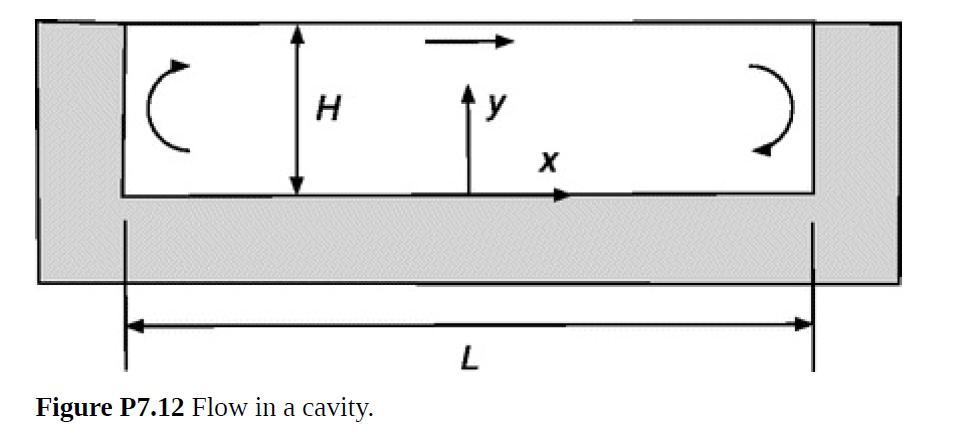

(a) By choosing an appropriate control volume, show that v_x averaged over the depth of the cavity must be zero for all x.

(b) Determine v_x(y) for the case in which the top surface is a solid plate sliding past the cavity at velocity U in the +x direction.

(c) Suppose now that y = H is a gas–liquid interface at which the temperature varies as

and that the temperature-dependence of the surface tension is described by

where β > 0. Assuming that viscosity variations are negligible, determine v_x(y) for this case. If ΔT = T_L − T₀ > 0, will the circulation be clockwise or counterclockwise? This is an example of a Marangoni flow.

Transcribed Image Text:

CTH P₂ y X Figure P7.12 Flow in a cavity. L