Refer to the three approximations derived for each of the four functions in Exercise 26. For each function use \(\mathrm{R}\) to construct a line plot of the function, along with the three approximations versus \(\delta\) on a single plot. The lines corresponding to each approximation and the original function should be different, that is, the plots should look like the one given in Figure 1.3. You may need to try several ranges of \(\delta\) to find one that provides a good indication of the behavior of each approximation. What do these plots suggest about the errors of the three approximations?

Exercise 26

Use Theorem 1.13 with \(p=1,2\) and 3 to find approximations for each of the functions listed below for small values of \(\delta\).

a. \(f(\delta)=1 /(1+\delta)\)

b. \(f(\delta)=\sin ^{2}(\pi / 4+\delta)\)

c. \(f(\delta)=\log (1+\delta)\)

d. \(f(\delta)=(1+\delta) /(1-\delta)\)

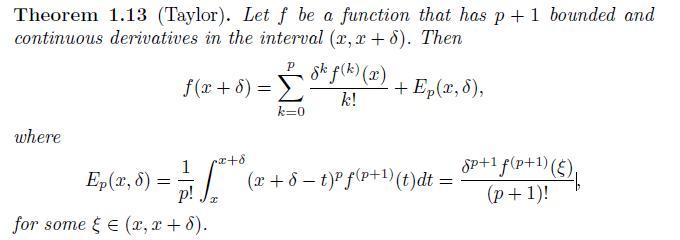
Figure 1.3

Transcribed Image Text:

P Theorem 1.13 (Taylor). Let f be a function that has p+1 bounded and continuous derivatives in the interval (x, x+6). Then f(x+8)= k=0 Sk f(k) (x) + Ep(x, 8), k! where 1 Ep(x, 8) = (x+8) f(p+1)(t)dt: = p! SP+1 f(p+1)() (p+1)! for some = (x, x + d).