Consider a model explaining the weekly sales ( \(S A L E S=100\) 's cans sold) of a popular brand (the "target" brand) of canned tuna as a function of its price ( \(P R I C E=\) average price in cents), the average prices of two competitors (PRICE2, PRICE3, also in cents). Also included is an indicator variable \(D I S P=1\) if there is a store display but no newspaper ad during the week for the target brand, and 0 otherwise. The indicator variable DISPAD \(=1\) if there is a store display during the week for the target brand and newspaper ads, 0 otherwise. The estimated log-linear model is

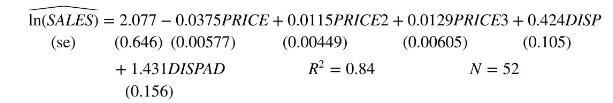
a. Discuss and interpret the coefficients of the price variables.

b. Are the signs and relative magnitudes of the advertising variables consistent with economic logic? Provide both the "rough" and "exact" calculations for the effects of DISP and DISPAD from Sections 7.3.1 and 7.3.2.

c. Test the significance of the advertising variables using a two-tail test, at the \(1 \%\) level of significance. What do you conclude?

d. The \(F\)-test statistic value for the joint significance of the two advertising variables is 42.0. What can we conclude about the significance of advertising? If you were going to use the form of the \(F\)-statistic in equation (6.4), what additional regression would you need to run?

e. Label the parameters in the equation \(\beta_{1}, \beta_{2}, \ldots\) If the null hypothesis is \(H_{0}: \beta_{6} \leq \beta_{5}\), state the alternative hypothesis. Why is the test of this null hypothesis and alternative hypothesis interesting? Carry out the test at the \(1 \%\) level of significance, given that the calculated \(t\)-value is 6.86. What do you conclude?

Data From Equation 6.4:-

Transcribed Image Text:

= In(SALES) 2.077 -0.0375PRICE+0.0115PRICE2 +0.0129PRICE3 +0.424DISP (se) (0.646) (0.00577) +1.431DISPAD (0.156) (0.00449) (0.00605) R2 = 0.84 N = 52 (0.105)