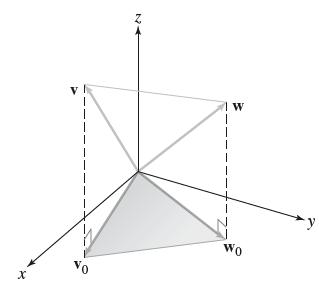
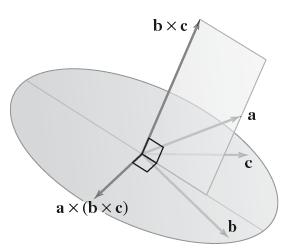
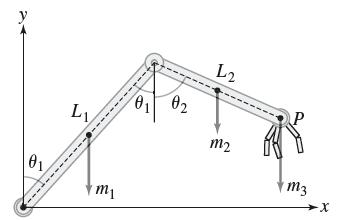
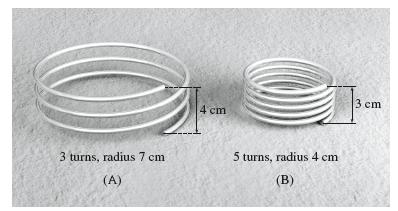
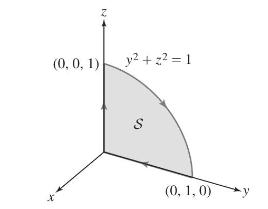
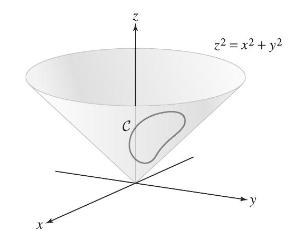
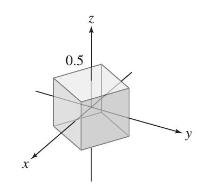
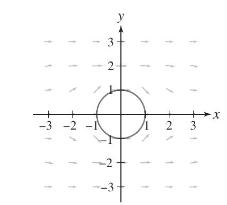
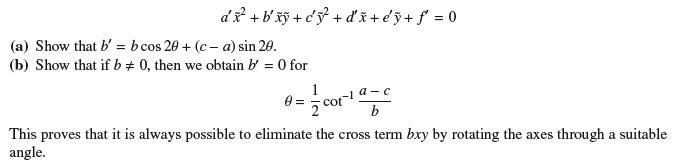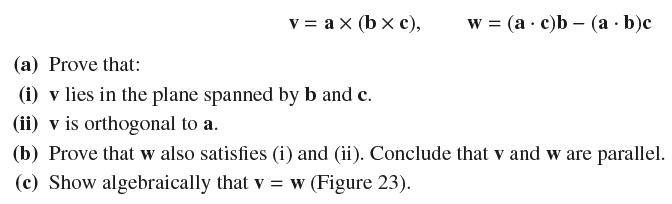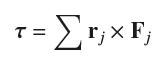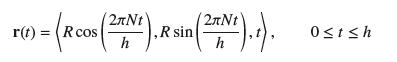Calculus 4th Edition Jon Rogawski, Colin Adams, Robert Franzosa - Solutions
Unlock a comprehensive understanding of "Calculus 4th Edition" by Jon Rogawski, Colin Adams, and Robert Franzosa with our extensive resource hub. Discover online answers key and detailed solutions manual, offering step-by-step answers to all questions. Access solutions PDF for solved problems, including test bank and chapter solutions. Our instructor manual provides insights and textbook solutions, ensuring thorough comprehension. Enjoy free download options for these invaluable resources, enhancing your learning with easy-to-follow explanations and comprehensive guidance. Ideal for anyone seeking expert-level understanding and assistance in calculus studies.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()