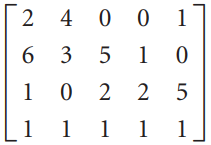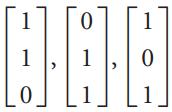![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


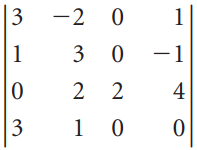

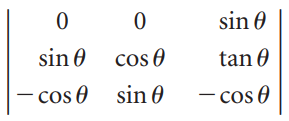
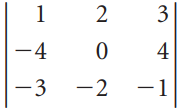
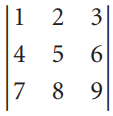
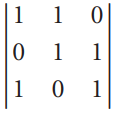
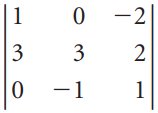
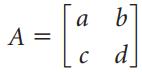
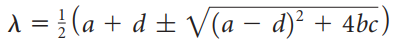
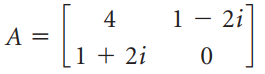
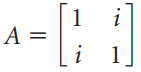
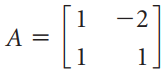
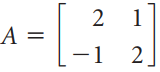
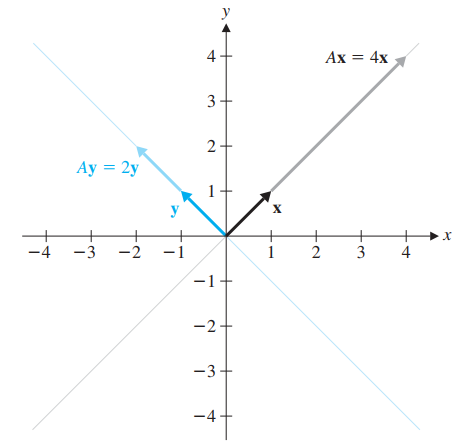

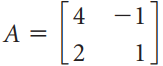

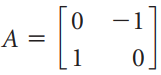

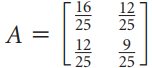
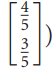
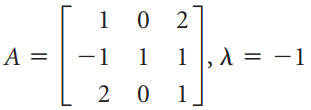
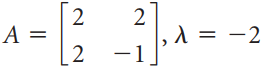
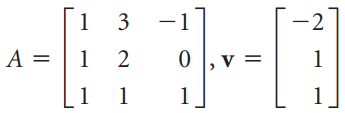
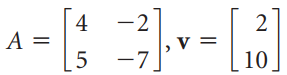
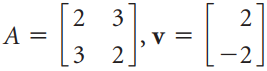
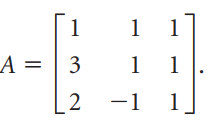
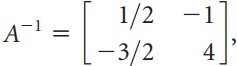
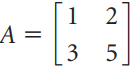
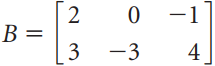
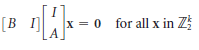
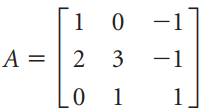
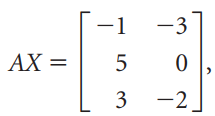

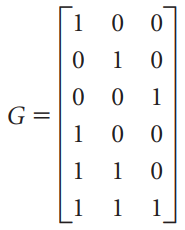
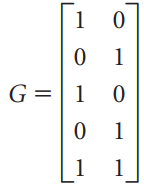
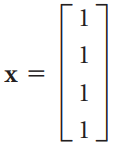
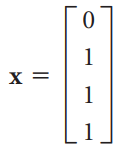
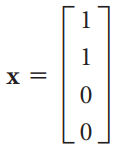
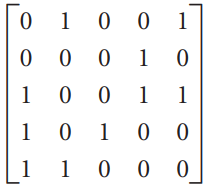

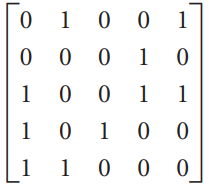
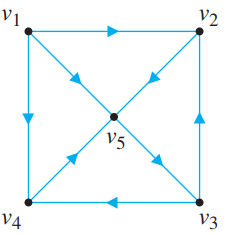
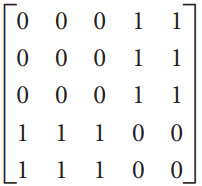
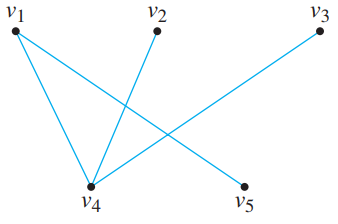
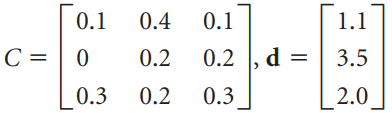
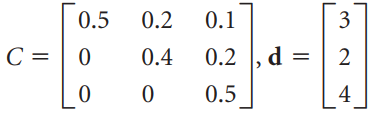

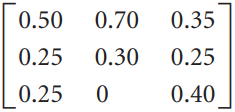

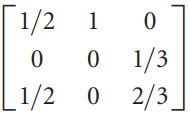
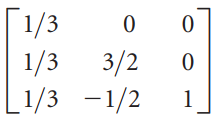
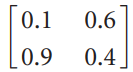
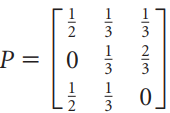

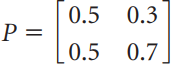
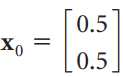
![х + 2х, — 3х, + х,] X1 У1 Ул + Зу style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/5/4/2/1775b8683a193cbd1535524486351.jpg)
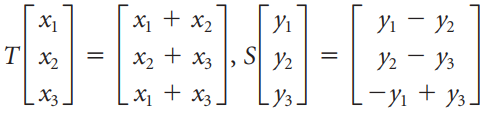
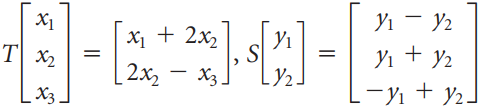
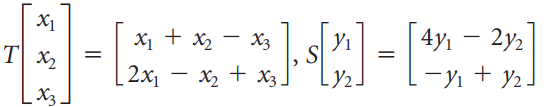
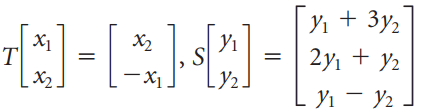
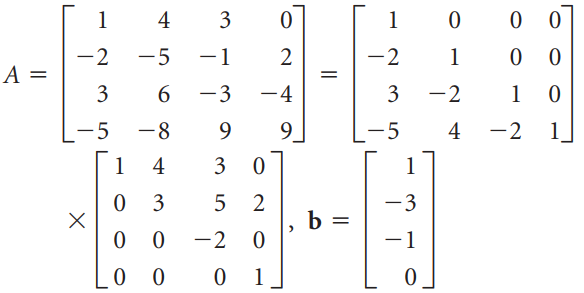
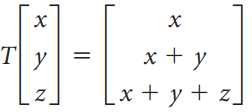
![х х — у +z 2х + у — 32]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/5/3/8/6725b8675f0e45051535520981750.jpg)
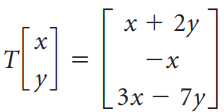

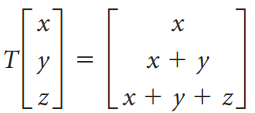
![х х — у+ z 2х + у — 32] T y - ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/5/3/8/2775b867465cf86a1535520586557.jpg)
![х+ 2у х — х У Зх — 7у]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/5/3/8/2485b867448ca41d1535520557323.jpg)