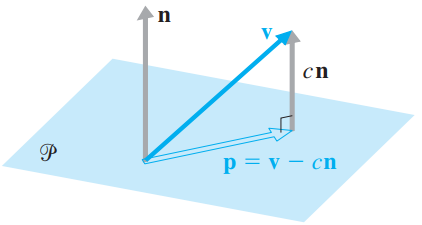
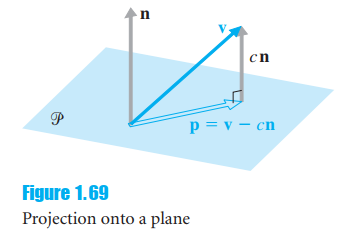
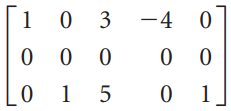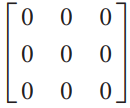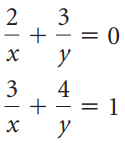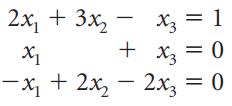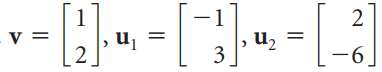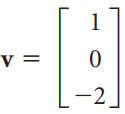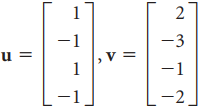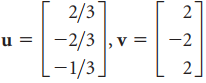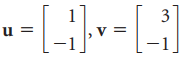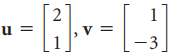![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


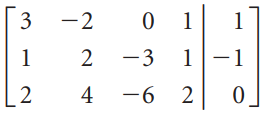
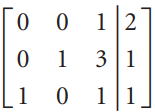
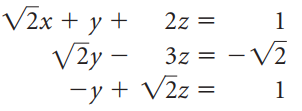
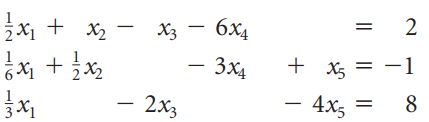
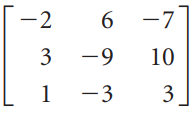
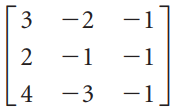
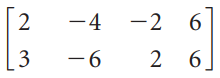


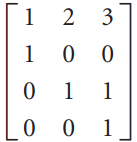
![1 0 0]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/1/2/1/1665b80170e39e871535103463401.jpg)