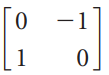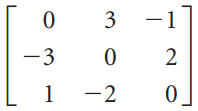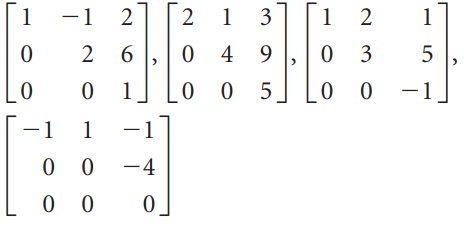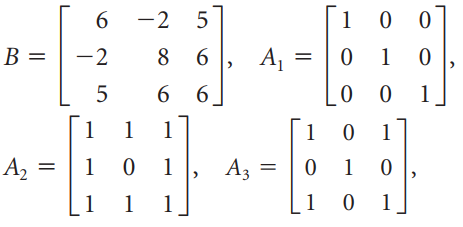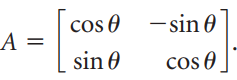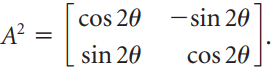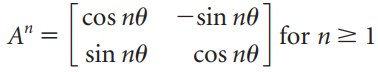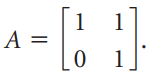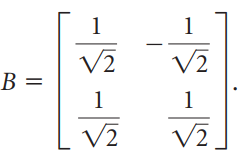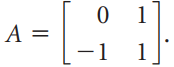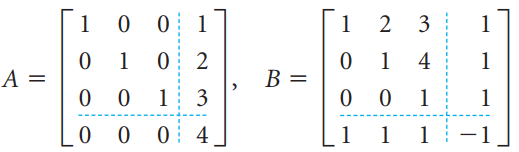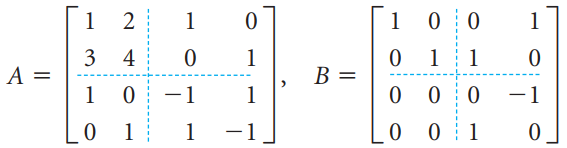![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


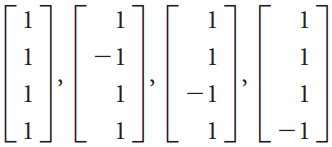
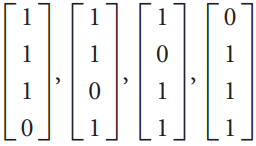

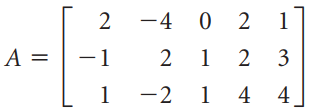
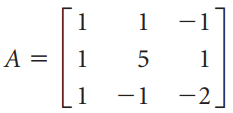
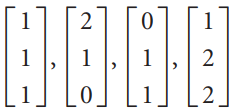

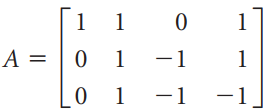
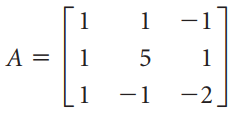
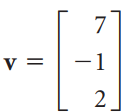
![-1 |A = 0 , b = [1 -3 -3] 3 3 -1 -5](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/6/9/3045b8566f85493d1535451609821.jpg)
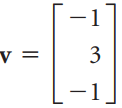
![3 = [-1 1 1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/6/9/2215b8566a5682101535451527065.jpg)
![-1 w = [1 -3] 3 -3 3 -5 -1 I|](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/6/9/1155b85663bbe4281535451420440.jpg)
![[1 -3 -3] 0 |, b |A = 3 %3D 3 -1 -5](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/6/9/0125b8565d4c06651535451318442.jpg)
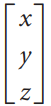
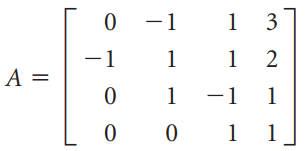
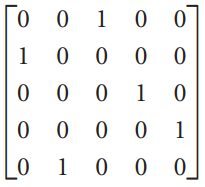
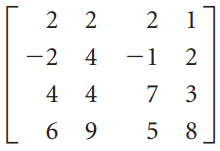
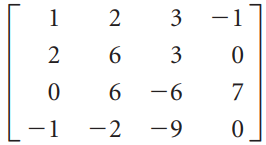
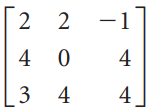
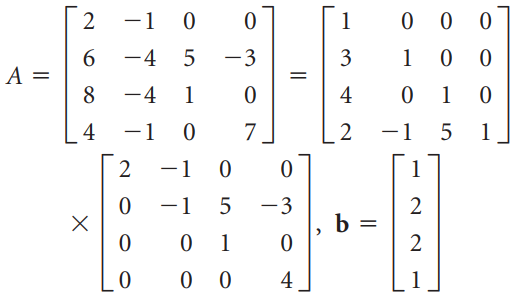
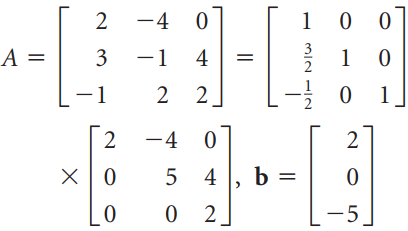
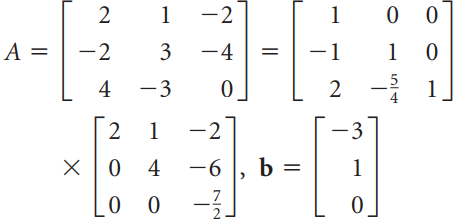
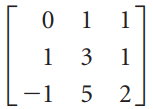
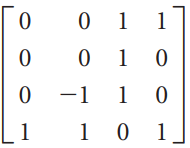
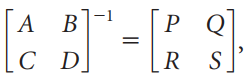
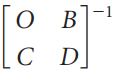
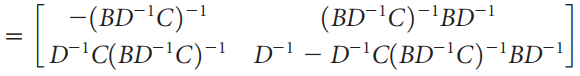
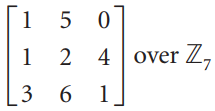
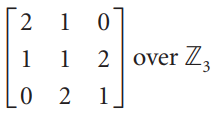
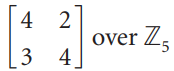
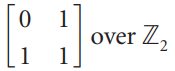
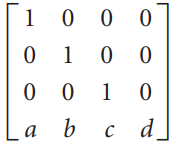
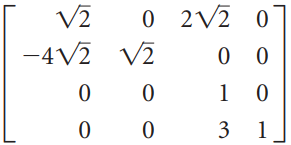

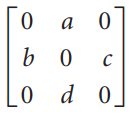
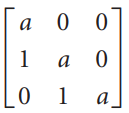
![_0 1 1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/5/1/4665b85214a24e021535433770644.jpg)
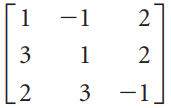

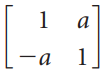
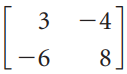

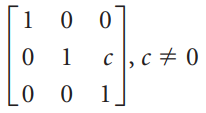
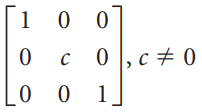
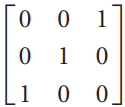

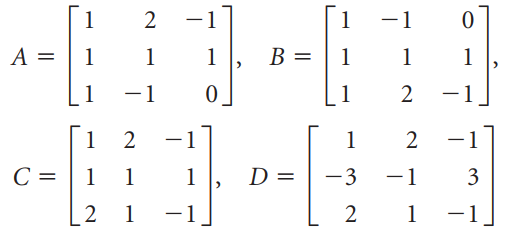
![1/а 1/Ь] 1/c 1/d](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/4/8/3775b8515396d5e41535430681953.jpg)
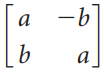
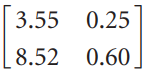
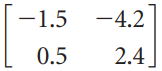
![[1/V2 -1/V2] L1/V2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/4/4/8/2485b8514b8461921535430552770.jpg)