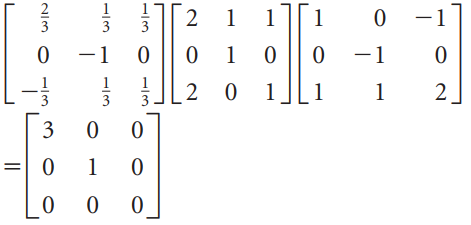
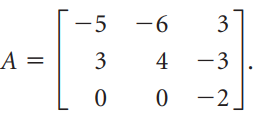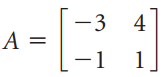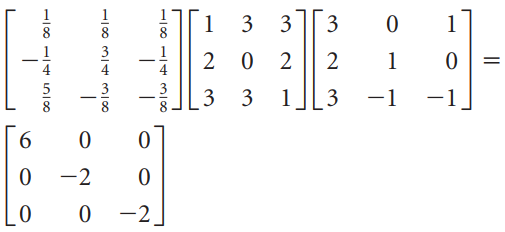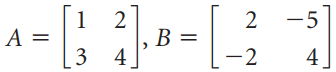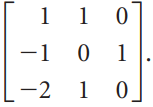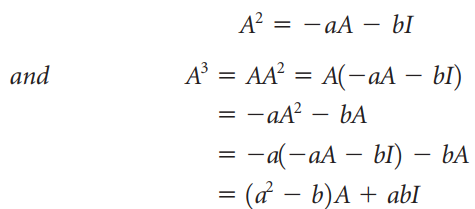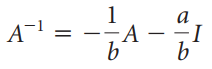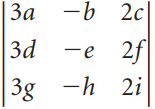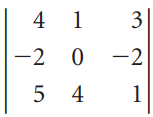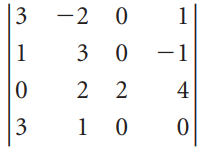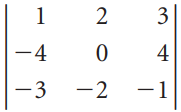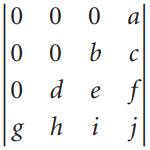![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


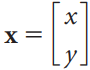
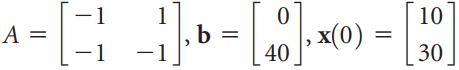
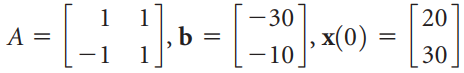
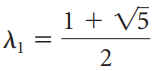
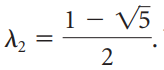
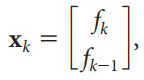
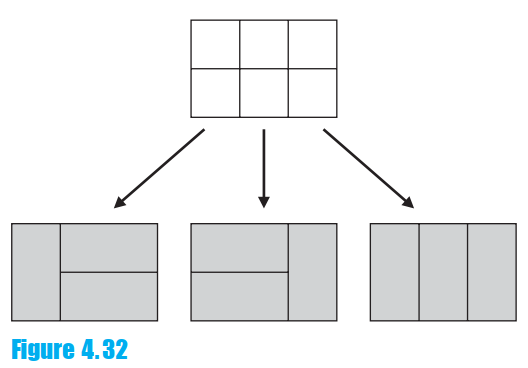
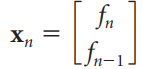
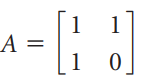
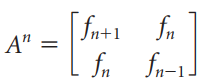
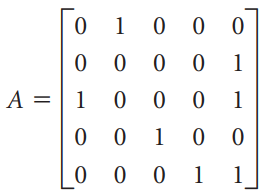
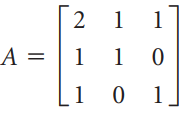

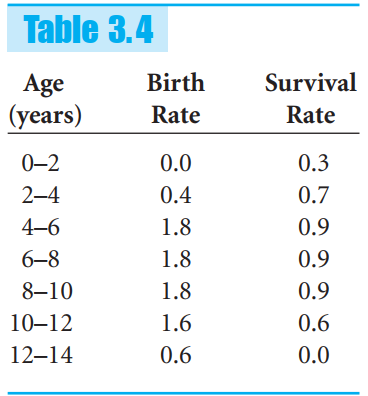

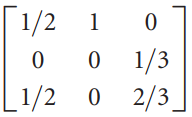
![1/3 2/3] 1/2 1/2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/7/3/3/0955b896d6792bec1535715412105.jpg)



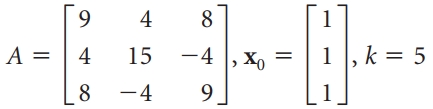
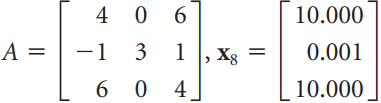
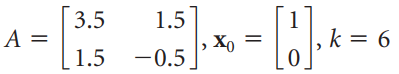
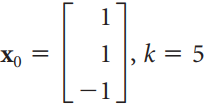
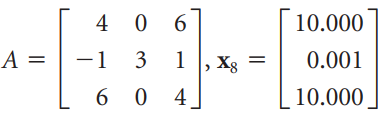
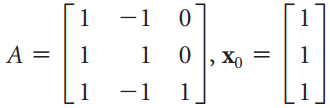
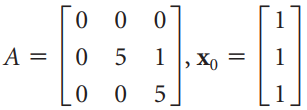
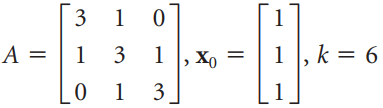
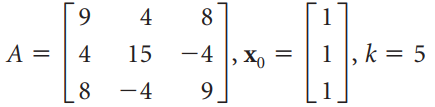
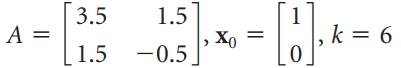
![3.415 -2 2.914 -3 X10 -1.207 1] -1 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/7/2/6/6105b895412c74021535708927100.jpg)
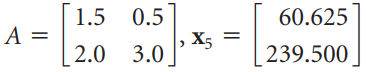
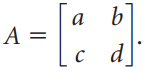
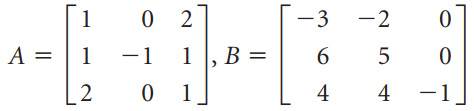
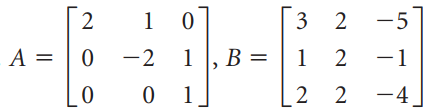
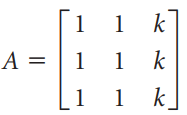
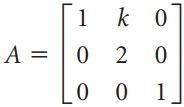
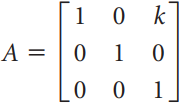
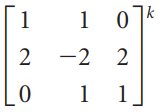
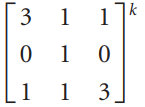
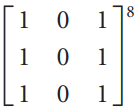
![]k 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/7/1/3/2795b891fff05e5c1535695595590.jpg)
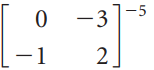
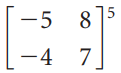
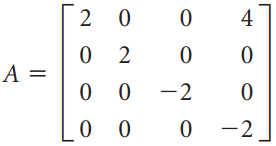
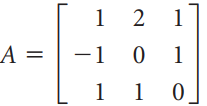
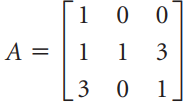
![A = 1 0]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/7/1/2/5755b891d3f3bde31535694892433.jpg)