(a) Show that the cruise-control feedback system described at the beginning of Box 22.2 has G(z) = 1/(1 iz) and H = /(iz), with z

(a) Show that the cruise-control feedback system described at the beginning of Box 22.2 has G̃(z) = 1/(1− iz) and H̃ = −κ/(iz), with z = ωτ and κ = Kτ, as claimed.

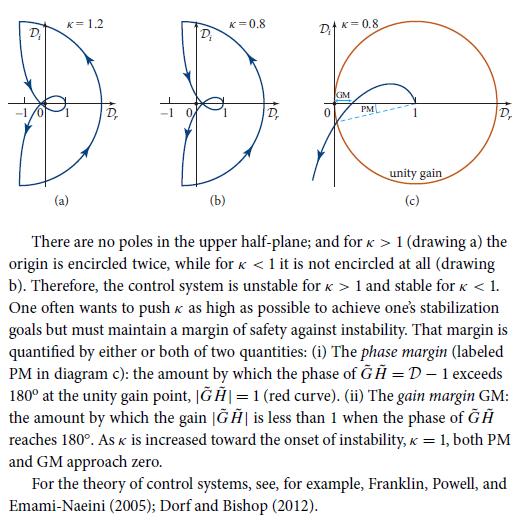
(b) Show that the Nyquist diagram has the forms shown in the second figure in Box 22.2, and that this control system is stable for all feedback strengthsκ >0.

(c) Solve explicitly for the zeros of D = 1 + G̃(z) H̃(z), and verify that none are in the upper half of the frequency plane.

(d) To understand the stability from a different viewpoint, imagine that the automobile’s speed v is oscillating with an amplitude δv and a real frequencyω around the desired speed V , v = V + δv sin(ωt), and that the feedback is turned off. Show that the output of the control system is

with a phase delay △φ = arctan(ωτ ) relative to the oscillations of v. Now turn on the feedback, but at a low strength, so it only weakly changes the speed’s oscillations in one period. Show that, because △φ 2)/dt is negative, so the feedback damps the oscillations. Show that an instability would arise if the phase delay were in the range π/2 △φ| △φ approaches π/2, so the cruise-control system is only marginally stable.

Box 22.2

uo = [/11+2] sin(t ),