Consider a gigantic container of gas made of identical particles that might or might not interact. Regard this gas as a bath, with temperature T_b and pressure P_b. Pick out at random a sample of the bath’s gas containing precisely N particles, with N >> 1. Measure the volume V of the sample and the temperature T inside the sample. Then pick another sample of N particles, and measure its V and T , and repeat over and over again. Thereby map out a probability distribution dp/dT dV for V and T of N-particle samples inside the bath.

(a) Explain in detail why

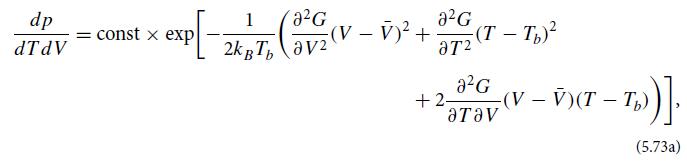
where G(N, T_b, P_b; T , V) = E(T , V , N) + P_bV − T_bS(T , V , N) is the out of equilibrium Gibbs function for a sample of N particles interacting with this bath, V̅ is the equilibrium volume of the sample when its temperature and pressure are those of the bath, and the double derivatives in Eq. (5.73a) are evaluated at the equilibrium temperature T_b and pressure P_b.

(b) Show that the derivatives, evaluated at T = T_b and V = V̅ , are given by 

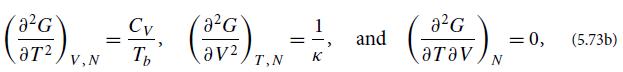
where C_V is the gas sample’s specific heat at fixed volume and κ is its compressibility at fixed temperature β, multiplied by V/P:

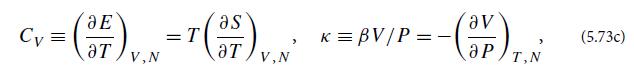
both evaluated at temperature T_b and pressure P_b. Thereby conclude that

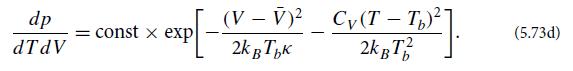
(c) This probability distribution says that the temperature and volume fluctuations are uncorrelated. Is this physically reasonable? Why?

(d) What are the rms fluctuations of the samples’ temperature and volume, σ_T and σ_V? Show that σ_T scales as 1/√N and σ_V as √N, where N is the number of particles in the samples. Are these physically reasonable? Why?

Transcribed Image Text:

dp dTdV 1 (8²G < exp[-24-7₂ (a1₂ (V - V73² + 2kBT av2 = const x exp a²G 372 (T - T₁)² a²G a Tav +2- (V - V)(T-T₂) (5.73a)