8.26. (Sec. 8.10.1) Bartlett-Nanda-Pillai V-test as a Bayes procedure. Let

"'1."'2"'" "'m+n be independently normally distributed with covariance matrix

! and means xE",; = 'Y;, i = 1, ... , m, ooE",; = 0, i = m + 1, ... , m + n. Let no be defined by [f I' l:] = [0, (J + CC') _. I], where the p X m matrix C has a density proportional to II + CC'I - hn+m), and fl = ('YI"'" 'Ym); let n l be defined by

[fl.l:]=[(J+CC')-IC,(J+CC,)-I] where C has a density proportional to II + CC'I- hn+m)e!!rc'u+cCY'c.

(a) Show that the measures are finite for n ~p by showing tr C'(J + CC,)-IC

"" cm), Dj = I + r,i~ I ciC; = EjE;, Cj = Ej _1 dj , j = 1, ... , m (Eo = J).

Show IDjl = IDj_11 (1 + d;dj ) and hence IDml = [I7'_ IO + i;d). Then refeI to Problem 5.15.]

(b) Show that the inequality (26) of Section 5.6 is equivalent to

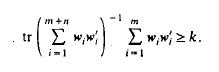
Hence the Bartlett-Nanda-Pillai V-test is Bayes and thus admissible.

Transcribed Image Text:

mtn m tr -1