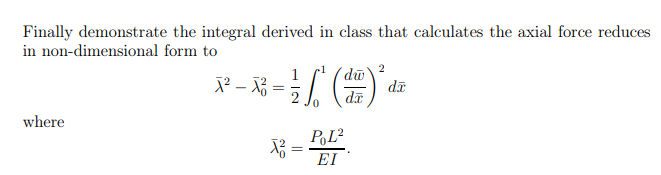
(1) In this problem, you will express the von Karman non-linear beam theory equations in non-dimensional form in order to facilitate subsequent solutions. It is natural to define a non-dimensional variable = x/L, where L is the length of the beam. The out-of- plane displacement can be normalized by the beam thickness, h, or by L. However a more convenient normalization for the out-of-plane displacement is to use the radius of gyration defined as rg = I/A, where I is the moment of inertia and A is the cross-sectional area of the beam. Therefore we will define the non-dimensional out-of-plane displacement as w = w A/I. Using these normalizations, derive the non-dimensional form of the governing equations for beams of constant EI. Further, consider the distributed force per unit length, q, to be the only external load. You should obtain the following expressions. d'u d where Q = -j2dw da q = X Q M d qL A EIV T In addition, the non-dimensional shear force, Q, and moment, M, are, respectively d w d+ dx = M du d = d'u dx where the non-dimensional shear force and non-dimensional moment are related to their dimensional counterparts as = 0 PL EI = +1 q dw d QL A EI R = KL and the non-dimensional slope and the non-dimensional curvature are related to their dimensional counterparts as ML A EI VI A dw I dx A Finally demonstrate the integral derived in class that calculates the axial force reduces in non-dimensional form to where 2 1 X - x = / (1) - 47 d 0 x = = PL EI