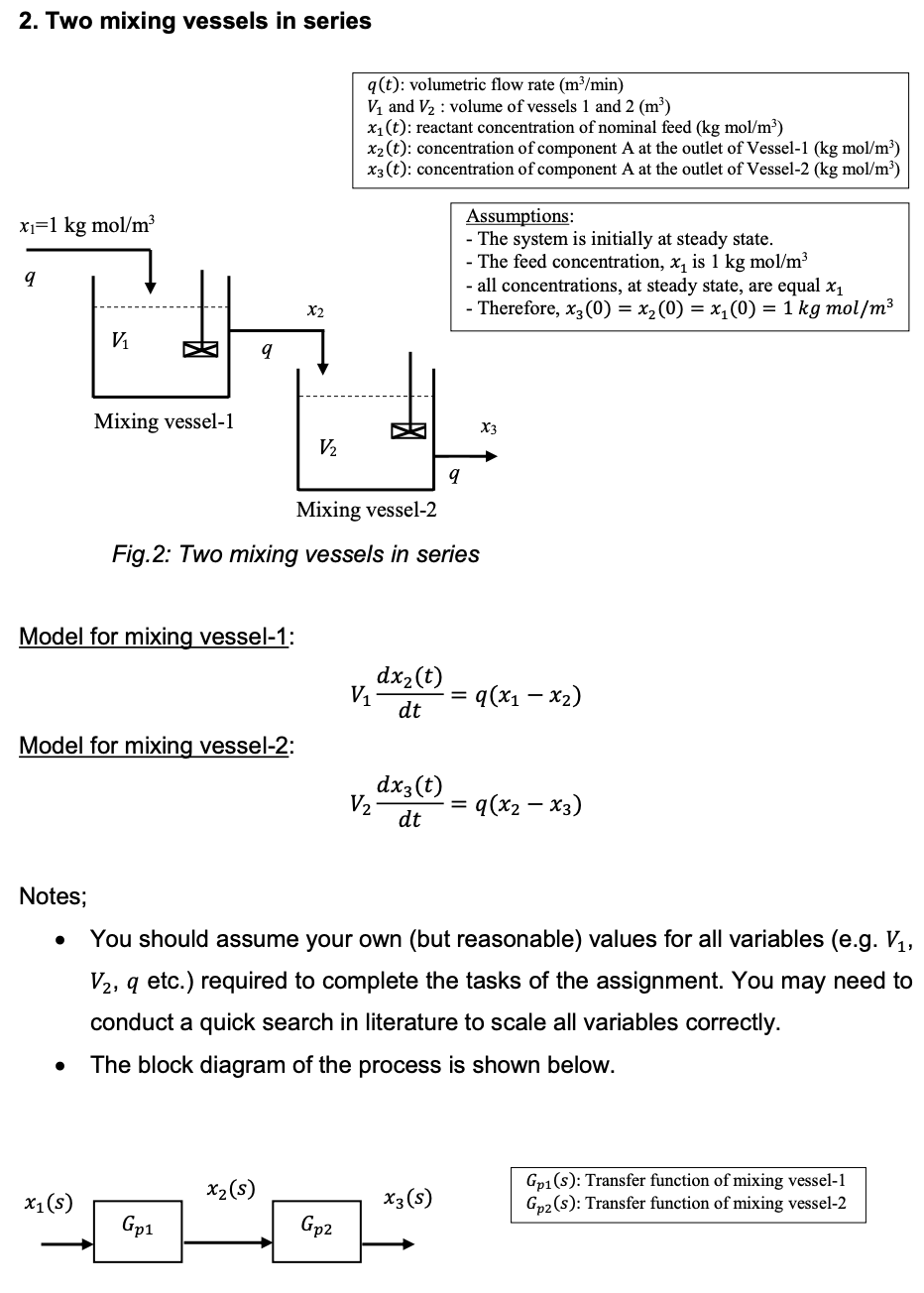
2. Two mixing vessels in series q(t): volumetric flow rate (m/min) V and V2: volume of vessels 1 and 2 (m) xi(t): reactant concentration of nominal feed (kg mol/m?) X2(t): concentration of component A at the outlet of Vessel-1 (kg mol/m) x3(t): concentration of component A at the outlet of Vessel-2 (kg mol/m?) xi=1 kg mol/m Assumptions: - The system is initially at steady state. - The feed concentration, x, is 1 kg mol/m all concentrations, at steady state, are equal x1 - Therefore, xz(0) = x2(0) = x1(0) = 1 kg mol/m3 9 X2 VA 9 Mixing vessel-1 X3 V2 9 Mixing vessel-2 Fig. 2: Two mixing vessels in series Model for mixing vessel-1: Vi dx2(t) = 9(x1 - x2) dt Model for mixing vessel-2: dxz(t) V2 = 9(x2 x3) dt Notes; . You should assume your own (but reasonable) values for all variables (e.g. V1, V2, q etc.) required to complete the tasks of the assignment. You may need to conduct a quick search in literature to scale all variables correctly. The block diagram of the process is shown below. . xz(s) x1(s) X3(s) Gpi(s): Transfer function of mixing vessel-1 Gpz(s): Transfer function of mixing vessel-2 Gp1 Gp2 = The model for a first mixer system (shown in Fig-2) is given by the following ODE; dx2(t) Vi 9(x1 - x2) dt where V1 is the volume of the first mixing vessel, x1 is the concentration at the feed, x2 is the concentration of component A at the outlet of the first mixing vessel and q is the volumetric flow rate. The above two equations can also be duplicated for the second mixing vessel using appropriate symbolsotations. [ You need to assume the reasonable values for all required variables, e.g. volumes, flow rate, etc.] Task-B1: Use Laplace transform to create the transfer function that describes the relationship between the outlet concentration X2(s) and the inlet concentration X1(s) for the first mixing vessel (i.e. X2(S) -). [Note: The initial condition (i.e. the concentrations at steady X1(s) state) is; x3(0) = x2(0) = x1(0) = 1 kg mol/m3). = = = Task-B2: Use Laplace transform to create the transfer function that describes the relationship between the two concentrations X2(s) and X3(s) for the second mixing vessel (i.e. X3 (). [Note: The initial condition is; x3(0) = x2(0) = x1(0) = 1 kg mol/m3]. ) X2 (S) = == Task-B3: Use Laplace transform to create the transfer function that describes the relationship between the outlet concentration of the second tank X3(s) and the inlet concentration Xa(s) of the first mixing vessel (i.e. 138). Note: The initial condition is;