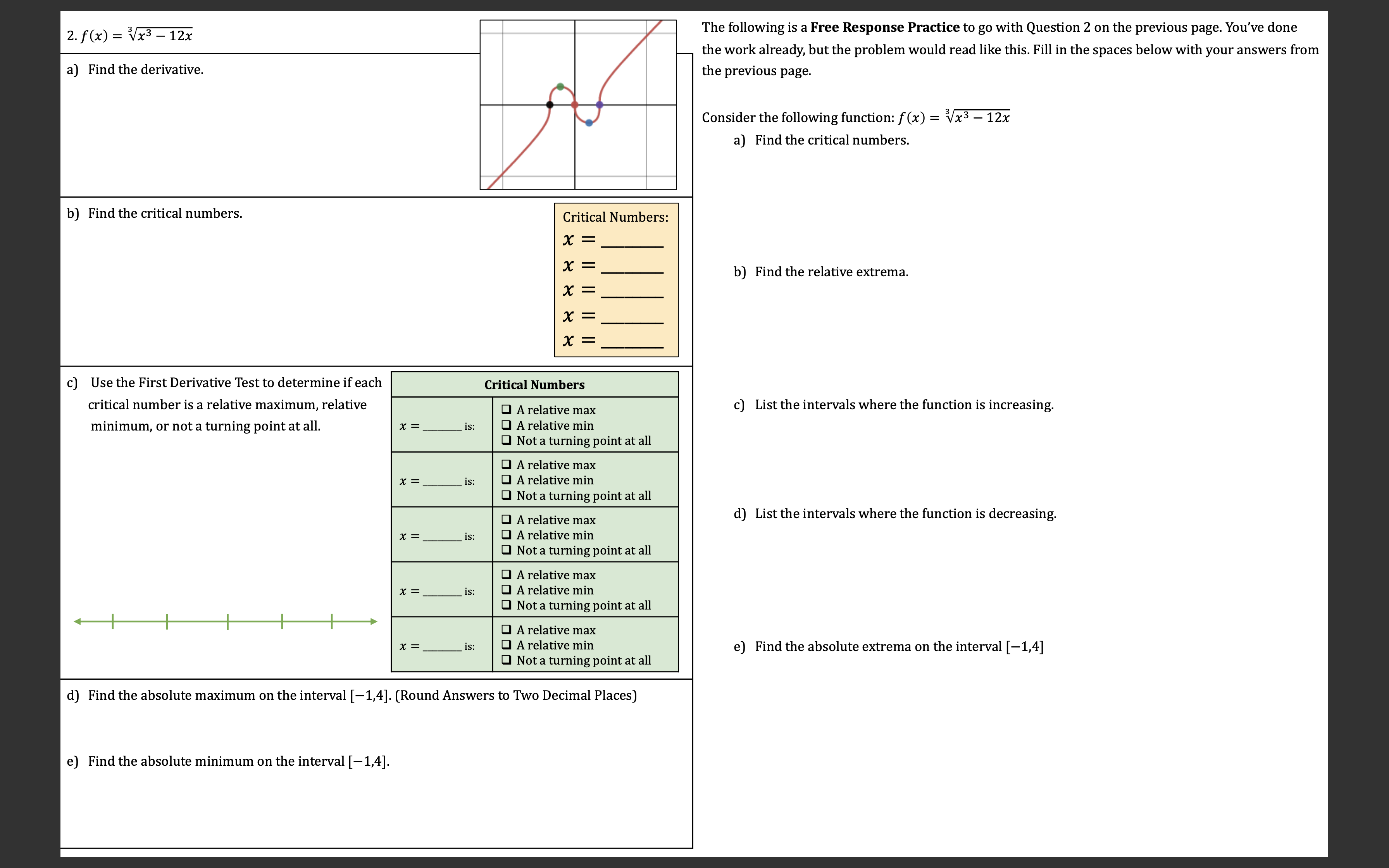
Question: calculus : please edit answers to image to make it as least confusing as possible or copy the format 2. f(x) = Vx3 - 12x

calculus : please edit answers to image to make it as least confusing as possible or copy the format
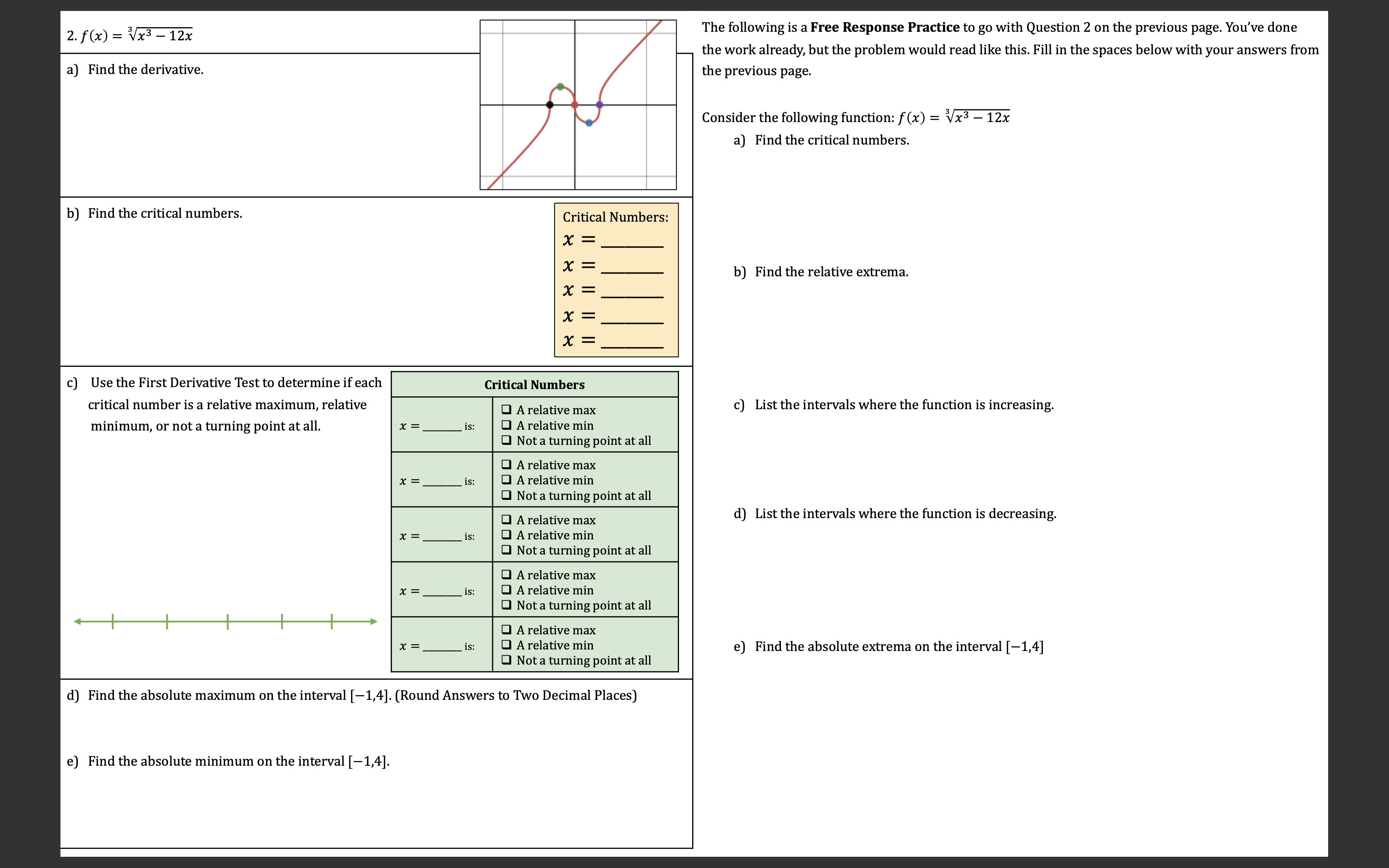

2. f(x) = Vx3 - 12x The following is a Free Response Practice to go with Question 2 on the previous page. You've done the work already, but the problem would read like this. Fill in the spaces below with your answers from a) Find the derivative. the previous page. Consider the following function: f (x) = Vx3 - 12x a) Find the critical numbers. b) Find the critical numbers. Critical Numbers: = X = b) Find the relative extrema. = X Y = Use the First Derivative Test to determine if each Critical Numbers critical number is a relative maximum, relative O A relative max c) List the intervals where the function is increasing. minimum, or not a turning point at all. * =_ is: O A relative min O Not a turning point at all A relative ma * =_ is O A relative mil O Not a turning point at all A relative ma d) List the intervals where the function is decreasing. X = is O A relative min O Not a turning point at all A relative ma X = _ is: O A relative mir Not a turning point at all A relative max X = is: O A relative min e) Find the absolute extrema on the interval [-1,4] O Not a turning point at all d) Find the absolute maximum on the interval [-1,4]. (Round Answers to Two Decimal Places) e) Find the absolute minimum on the interval [-1,4].Summarize Concepts: 1. By Fermat's Stationary Points Theorem, turning points for a function f (relative extrema) can only occur if the derivate of the function is either or 2. If a function f is increasing at x = c, then the function's derivative is at x = c. 3. If a function f is decreasing at x = c, then the function's derivative is at x = c. 4. If a function changes from increasing to decreasing at x = c, then Increasing to the derivative must change from to Decreasing at x = C at x = c, and so by the First Derivative Test there must be a relative x = C. Sketch the signs on the provided number line. 5. If a function changes from decreasing to increasing at x = c, then Decreasing to the derivative must change from to Increasing at x = c at x = c, and so by the First Derivative Test there must be a relative. x = C. Sketch the signs on the provided number line. 6. To use the First Derivative Test, you should draw a and label the critical numbers from least to greatest. Then, plug in test-points on each interval to determine if the derivative is or 7. To find absolute extrema on a closed interval [a, b], you should evaluate the function at the turning points and at the of the interval. 8. Suppose a function's derivative is given by the rule f' (x) = 2x(x -5)2(x + 1) Determine if the function f is increasing or decreasing at each of the following points: a) At x = 3, the function is b) At x = 2, the function is c) Atx = -0.5, the function is d) At x = -3, the function is e) At x = 6, the function is f) What is happening at x = 0, x = 5, x = -1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


