Mil2k1

Please answer all the question.

1)

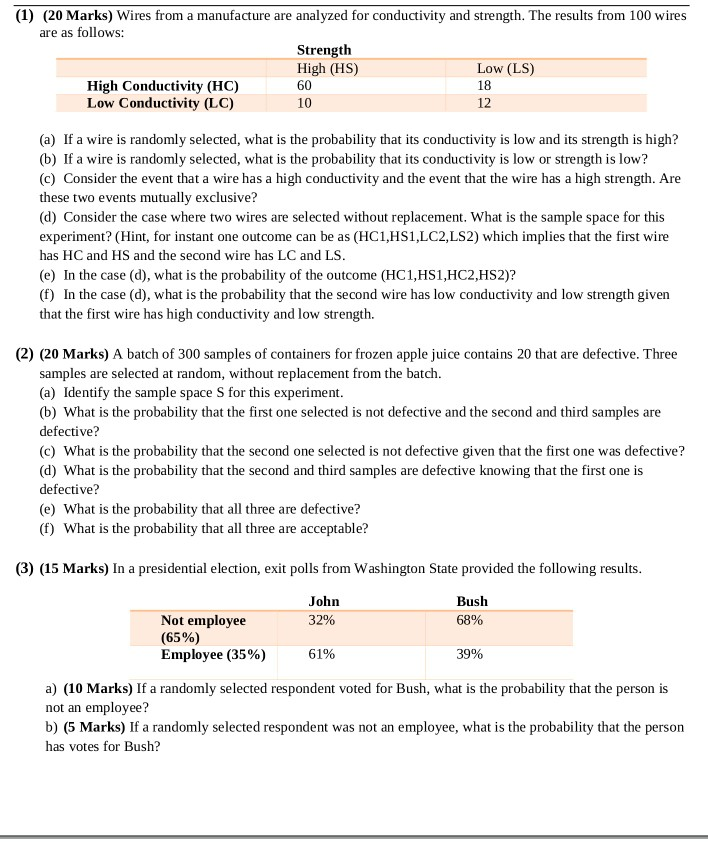
2. There are 100 boys and 100 girls in a dance party. (1) Each boy was introduced to 2 girls, and each girl was introduced to 2 boys. Is it possible to group 100 pairs such that the two partners in each pair have been int-reduced to each other ? (Hint : You might use Birkhoff's theorem : every doubly stochastic matrix is the convex envelop of permutation matrices.) (2) The party starts at 8 pm and ends at 11 pm. If the pair 2' and 3' dance for time tij, their happiness is fig-132} for some 7 > 0. Here 1* can be interpreted as the lassitude of participants. The goal is to maximize the total happiness of participants. (a) Formulate the optimization problem. (b) For what Values of 7 should everyone stick to his /her initial partner ? [1] {so Marks] Wires from a manufacture are analyzed for conduuivity and strength. The results from lil wires are as follows: 59191135!\" _ . . High (HS) Low (LS) High Conductivity {HC} El] 13 Low Conductivity [LC] ll] 12 [a] If a wire is randotttly selected, what is the probability that its conductivity is low and its strength is high? [b] If a wire is randomly selected, what is the probability that its conductivity is low or strength is low? [cl Consider the event that a wire has a high conductivity and the event that the wire has a high strength. Are these two events mutually exclusive? [d] Consider the case where two wires are selected without replacement. What is the sample space for this experiment? (Hint, for instant one outcome can be as [HC1,HSI,LC2,L52] which implies that the first wire has HC and HS and the second wire has LC and LS. (e) In the case [d], what is the probability of the outcome {HC 1,H51,HC2,H52]? [f] In the case [d], what is the probability that the second wire has low conductivity and low strength given that the first wire has high conductivity and low strength. [2] {2n Marks] A. batch of Slit] samples of containers for frozen apple juice contains 2t] that are defective. Three samples are selected at random, without replacement from the batch. (a) Identify the sample space S for this experiment. (b) What is the probability that the rst one selected is not defective and the second and third samples are defective? [c] What is the probability that the second one selected is not defective given that the rst one was defective? (d) What is the probability that the second and third samples are defective knowing that the rst one is defective? (e) What is the probability that all three are defective? [f] What is the probability that all three are acceptable? [3] [15 Marks] In a presidential election, exit polls from Washington State provided the following results. . . ._ . Jsh." has]; Not _ployee 32% 53% [65%] Employee (35%] 51% 39% a] [1i] Marks] If a randomly selected respondent voted for Bush, what is the probability that the person is not an employee? b] [5 Marks} If a randomly selected respondem was not an employee, what is the probability that the person has votes for Bush? A small regional carrier accepted 16 reservations for a particular flight with 12 seats. 10 reservations went to regular customers who will arrive for the flight. Each of the remaining passengers will arrive for the flight with a 44% chance, independently of each other. Find the probability that overbooking occurs. Preview Find the probability that the flight has empty seats. Preview Points possible: 2 License Unlimited attempts. Score on last attempt: (0, 0), Score in gradebook: (0, 0), Out of: (1, 1) Message instructor about this question2) Match each sampling technique with the appropriate description. Write the correct letter in the space provided. (2 points each) Cluster a) Select every 20th member of the population Convenience b) May lead to bias Simple Random Sample c) Break the population into smaller groups, then randomly select entire groups Stratified d) Break the population into smaller groups, then randomly select members from each group Systematic e) Number the entire population, then randomly select numbers 3) Suppose a data set has a minimum value of 45 and a maximum value of 100. What would the class width be if we wanted to split the data into 6 classes? (20 points)Independent events Example 6: A vehicle contains two engines, a main engine and a backup. The engine component fails only if both engines fail. The probability that the main engine fails is 0.05, and the probability that the backup engine fails is 0.10. Assume that the main and backup engines function independently. What is the probability that the engine component fails? Example 7: A system contains two components, A and B. Both components must function for the system to work. The probability that component A fails is 0.08, and the probability that component B fails is 0.05. Assume the two components function independently. What is the probability that the system functions