Question
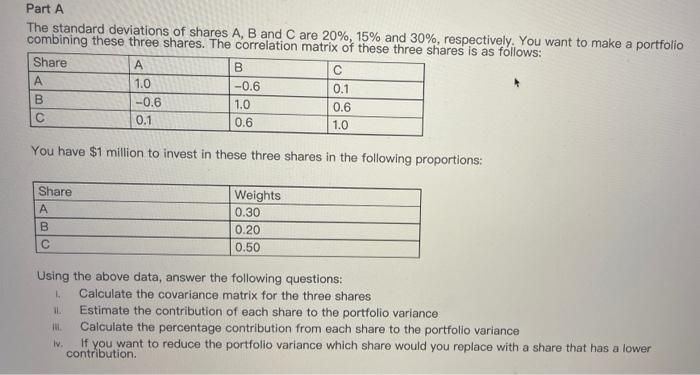
Part A The standard deviations of shares A, B and C are 20%, 15% and 30%, respectively. You want to make a portfolio combining these
Part A
The standard deviations of shares A, B and C are 20%, 15% and 30%, respectively. You want to make a portfolio combining these three shares. The correlation matrix of these three shares is as follows:
Share | A | B | C |
A | 1.0 | -0.6 | 0.1 |
B | -0.6 | 1.0 | 0.6 |
C | 0.1 | 0.6 | 1.0 |
You have $1 million to invest in these three shares in the following proportions:
Share | Weights |
A | 0.30 |
B | 0.20 |
C | 0.50 |
Using the above data, answer the following questions:
- Calculate the covariance matrix for the three shares
- Estimate the contribution of each share to the portfolio variance
- Calculate the percentage contribution from each share to the portfolio variance
- If you want to reduce the portfolio variance which share would you replace with a share that has a lower contribution.
Part B - Derivative applications
You are interested in creating a levered version of an ETF. The ETF has a Sharpe ratio of 0.70 and an annual return standard deviation of 30%. The risk free rate is 4%. You have $100,000 to invest. You want to borrow $400,000 at the risk free rate and invest the total amount in the ETF. Calculate the expected return and Sharpe ratio of the levered portfolio and compare the Sharpe ratio of the levered portfolio with the above Sharpe ratio.

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


