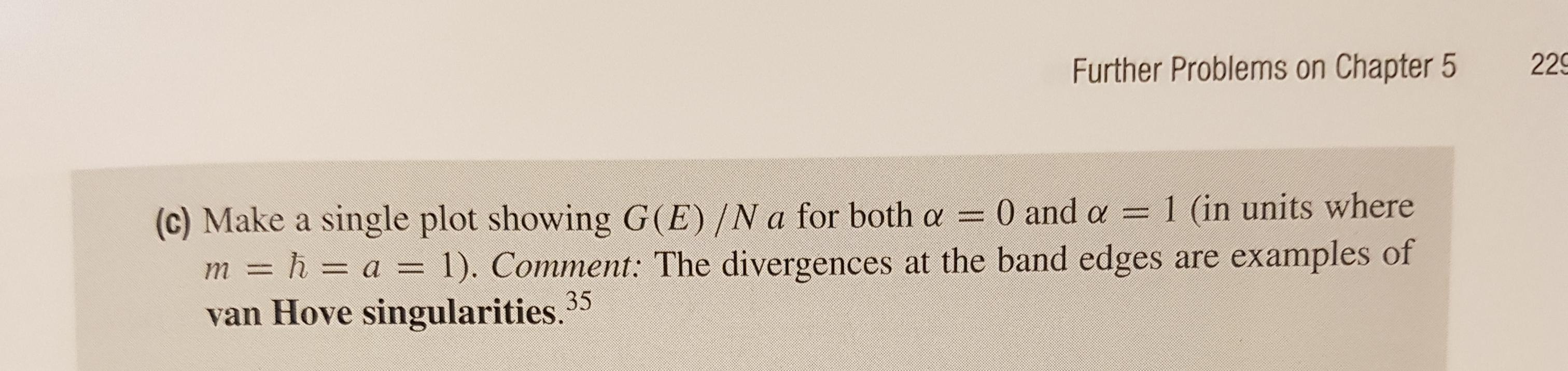
Problem 5.37 An important quantity in many calculations is the density of states G(E): G(E) dE = number of states with energy between E and E + dE. For a one-dimensional band structure, G(E) DE = 2 where dq/(2T/N a) counts the number of states in the range dq (see Equation 5.63), and the factor of 2 accounts for the fact that states with q and -q have the same energy. Therefore 1 1 1 dE/dq| (a) Show that for a = 0 (a free particle) the density of states is given by G(E) dq (27/(Na). = 1 (b) Find the density of states for a #0 by differentiating Equation 5.71 with respect to q to determine dE/dq. Note: Your answer should be written as a function of E only (well, and a, m, h, a, and N) and must not contain q (use k as a shorthand for 2mE/h, if you like). G free (E) - m ThV 2E Further Problems on Chapter 5 225 (c) Make a single plot showing G(E) /N a for both a = 0 and a = 1 (in units where m = h = a = 1). Comment: The divergences at the band edges are examples of van Hove singularities.35