Compare the wave functions for the first three energy levels for a particle in a box of width L (see Fig. 40.12a) to the corresponding wave functions for a finite potential well of the same width (see Fig. 40.15a). How does the wavelength in the interval 0 ‰¤ x ‰¤ L for the n = 1 level of the particle in a box compare to the corresponding wavelength for the n = 1 level of the finite potential well? Use this to explain why E₁is less than E_1-IDWin the situation depicted in Fig. 40.15b.

Fig.40.12a

Fig.40.15

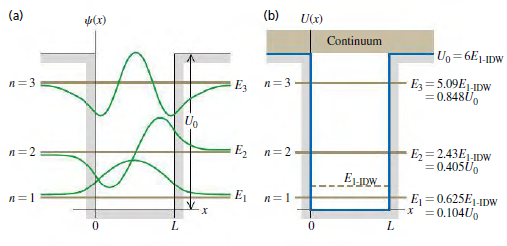
(a) (b) UCx) (x) Continuum Uo=6E1-1Dw E=5.09E1-1Dw = 0.848U, n=3 E, n=3 Ug , 32 E = 2.43E1-IDW = 0.405U0 _Euow. E1 Ej = 0.625E1-1DW x =0.1040o n=1 n=1