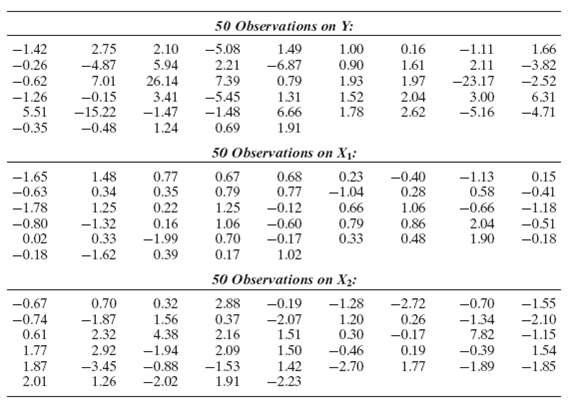
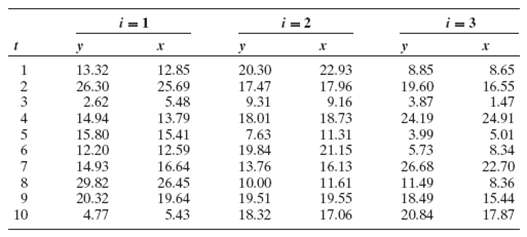
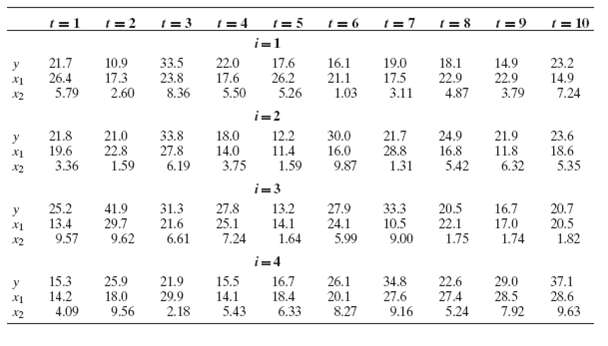
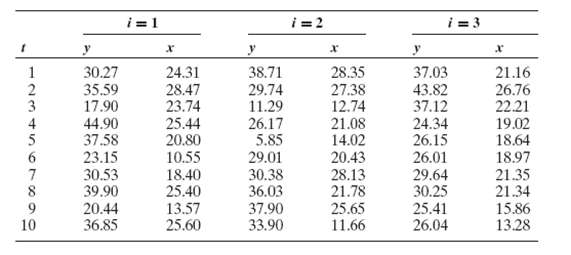
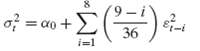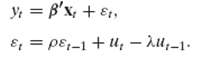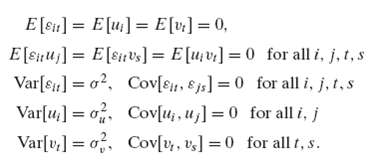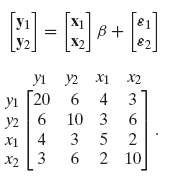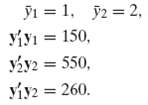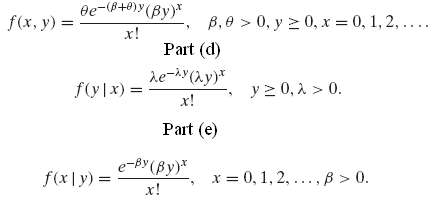Econometric Analysis 5th Edition William H. Greene - Solutions
Discover the comprehensive solutions to "Econometric Analysis 5th Edition" by William H. Greene. Access a complete answers key and solutions PDF, providing detailed answers to every question. Our solution manual offers step-by-step answers, ensuring a thorough understanding of solved problems. Explore our instructor manual, test bank, and chapter solutions for an enhanced learning experience. This valuable resource is ideal for those seeking textbook solutions and questions and answers for academic success. Enjoy free download options for easy access and improve your econometric skills with our expertly crafted materials.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


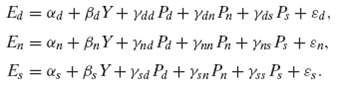
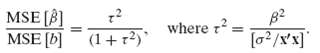
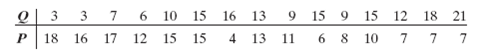
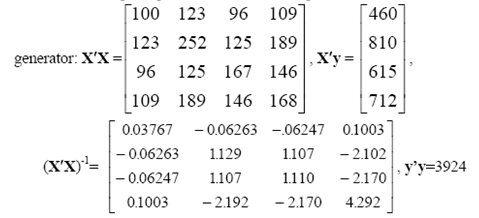
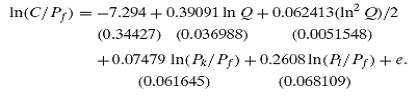
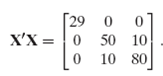
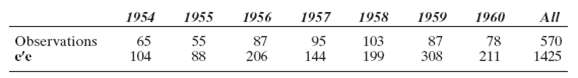
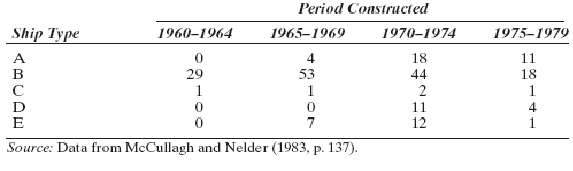

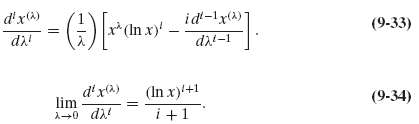
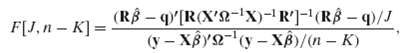
![s2 Est. Var[ÿ] = s²X'X)-' =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/7/2/1645c7688e40526e1551272164062.jpg)