The feed to a pair of gas permeators connected with retentate in series is \(40 \mathrm{~mol} \%\) carbon dioxide and 60 \(\mathrm{mol} \%\) nitrogen. The perfectly mixed membrane separators are equipped with silicone rubber membranes with effective membrane thicknesses of \(0.9 \mu \mathrm{m}\). In both units, the pressure on the permeate side is \(1.07 \mathrm{bar}\) and the retentate pressure is \(5.3 \mathrm{bar}\). The membrane units operate at \(25^{\circ} \mathrm{C}\). Feed rate to the first unit is \(120.0 \mathrm{kmol} / \mathrm{h}\). Assume an ideal gas. Data are in Table 19-2.

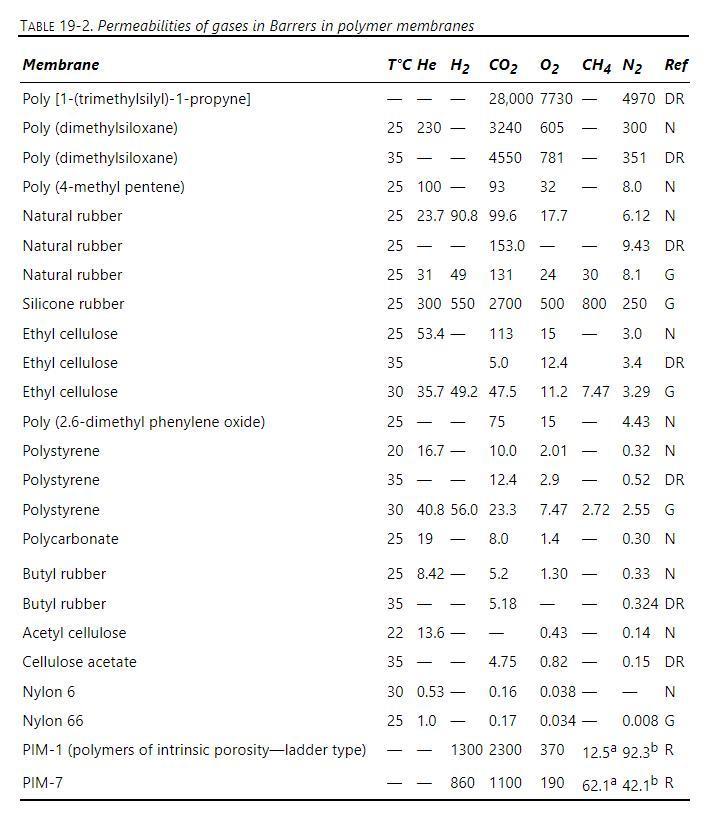
a. Can a single unit produce the desired retentate with \(\mathrm{y}_{\mathrm{r}, \mathrm{CO} 2}=0.16\) ?

b. Whether or not a single membrane will work, design a system with two units in series because a higher flow rate of desired retentate can be obtained. We want the retentate from the second membrane unit to be \(\mathrm{y}_{\mathrm{r} 2, \mathrm{CO} 2}=0.16\). Design the system (provide values of \(\theta_{1}\) and \(\theta_{2}\) and report resulting values of \(\mathrm{F}_{\mathrm{r} 1}, \mathrm{~F}_{\mathrm{r} 2}, \mathrm{y}_{\mathrm{p} 1}\), \(\mathrm{y}_{\mathrm{r} 1}, \mathrm{y}_{\mathrm{p} 2}\), and \(\mathrm{y}_{\mathrm{r} 2}\) ) to obtain the highest flow rate of retentate gas \(\left(\mathrm{F}_{\mathrm{r} 2}\right)\) as possible.
If the equations are set up in a spreadsheet, first find the value of \(\mathrm{y}_{\mathrm{p} 2}\) that corresponds to specified \(\mathrm{y}_{\mathrm{r} 2}\). A case study approach (pick a value of \(\mathrm{y}_{\mathrm{p} 1}\), calculate \(\mathrm{y}_{\mathrm{r} 1}=\mathrm{y}_{\mathrm{in}, 2}\) from the RT equation, calculate \(\theta_{1}\) and \(\theta_{2}\), then find \(\mathrm{F}_{\mathrm{r} 2}\) and repeat for different values of \(\mathrm{y}_{\mathrm{p} 1}\) ) works well.
\(\mathrm{y}_{\mathrm{p} 1}, \mathrm{y}_{\mathrm{r} 1}, \mathrm{y}_{\mathrm{p} 2}\), and \(\mathrm{y}_{\mathrm{r} 2}\) are mole fractions of the faster permeating gas.

Transcribed Image Text:

TABLE 19-2. Permeabilities of gases in Barrers in polymer membranes TC He H2 CO2 O2 CH4 N2 Ref Membrane Poly [1-(trimethylsilyl)-1-propyne] Poly (dimethylsiloxane) Poly (dimethylsiloxane) Poly (4-methyl pentene) Natural rubber Natural rubber 25 100 Natural rubber Silicone rubber Ethyl cellulose Ethyl cellulose Ethyl cellulose Poly (2.6-dimethyl phenylene oxide) Polystyrene Polystyrene Polystyrene Polycarbonate Butyl rubber Butyl rubber Acetyl cellulose Cellulose acetate Nylon 6 Nylon 66 PIM-1 (polymers of intrinsic porosity-ladder type) PIM-7 28,000 7730 - 4970 DR 25 230 - 3240 605 300 N 35 - - 4550 781 351 DR 93 32 - 8.0 N 25 23.7 90.8 99.6 17.7 6.12 N 25 - - 153.0 9.43 DR 25 31 49 131 24 30 8.1 G 25 300 550 2700 25 53.4- 113 35 500 800 250 G 15 - 3.0 N 5.0 12.4 3.4 DR 30 35.7 49.2 47.5 11.2 7.47 3.29 G 25 - - 75 15 4.43 N 20 16.7 - 10.0 2.01 - 0.32 N 35 - - 12.4 2.9 - 0.52 DR 30 40.8 56.0 23.3 7.47 2.72 2.55 G 25 19 - 8.0 1.4 - 0.30 N 25 8.42 5.2 1.30 0.33 N 35 - 5.18 - 0.324 DR 22 13.6- - 0.43 0.14 N 35 - - 4.75 0.82 0.15 DR 30 0.53- 0.16 0.038- N 25 1.0 - 0.17 0.034 0.008 G 1300 2300 370 12.5a 92.3b R ] 860 1100 190 62.1a 42.1b R