The objective of this problem is to use Verilog to describe and simulate a multiplier for signed binary numbers using Booth€™s algorithm. Negative numbers should be represented by their 2€™s complement. Booth€™s algorithm works as follows, assuming each number is n bits including sign: Use an (n + 1) -bit register for the accumulator 

(A) So the sign bit will not be lost if an overflow occurs. Also, use an (n + 1)-bit register.

(B) To hold the multiplier and an n-bit register.

(C) To hold the multiplicand.

1. Clear A (the accumulator), load the multiplier into the upper n bits of B, clear B₀, and load the multiplicand into C.
2. Test the lower two bits of B (B₁B₀). If B₁B₀ = 01, add C to A (C should be sign-extended to n + 1 bits and added to A using an (n + 1)-bit adder).
If B₁B₀ = 10, add the 2€™s complement of C to A. If B₁B₀ = 00 or 11, skip this step.
3. Shift A and B together right one place with sign extended.
4. Repeat steps 2 and 3, n - 1 more times.
5. The product will be in A and B, except ignore B₀.

Example for n = 5: Multiply 29 by -13.

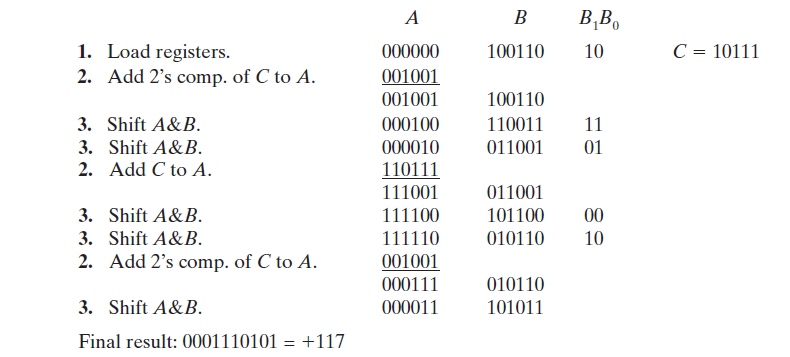
(a) Draw a block diagram of the system for n = 8. Use 9-bit registers for A and B, a 9-bit full adder, an 8-bit complementer, a 3-bit counter, and a control circuit. Use the counter to count the number of shifts.
(b) Draw a state graph for the control circuit. When the counter is in state 111, return to the start state at the time the last shift occurs (three states should be sufficient).
(c) Write behavioral Verilog code for the multiplier. 

(d) Simulate your Verilog design using the following test cases (in each pair, the second number is the multiplier):

01100110 × 00110011
10100110 × 01100110

B B,B, 1. Load registers. 2. Add 2's comp. of C to A. C = 10111 000000 100110 10 001001 001001 100110 11 3. Shift A&B. 000100 110011 3. Shift A&B. 000010 011001 01 110111 2. Add C to A. 111001 011001 3. Shift A&B. 111100 101100 00 3. Shift A&B. 111110 010110 10 Add 2's comp. of C to A. 2. 001001 000111 010110 3. Shift A&B. 000011 101011 Final result: 0001110101 = +117