Suppose that (X) is a (operatorname{PoIsson}(lambda)) random variable, so that the moment generating function of (X) is
Question:
Suppose that \(X\) is a \(\operatorname{PoIsson}(\lambda)\) random variable, so that the moment generating function of \(X\) is \(m(t)=\exp \{\lambda[\exp (t)-1]\}\). Find the cumulant generating function of \(X\), and put it into the form given in Equation (2.24). Using the form of the cumulant generating function, find a general form for the cumulants of \(X\).
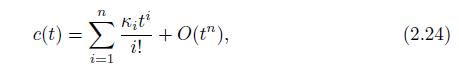
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





