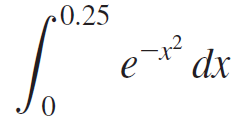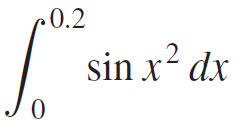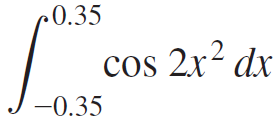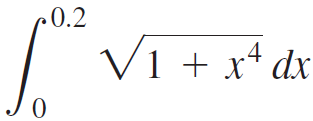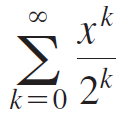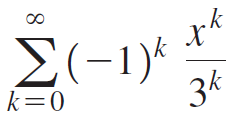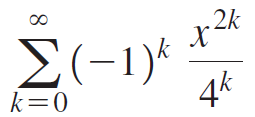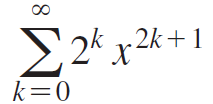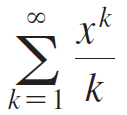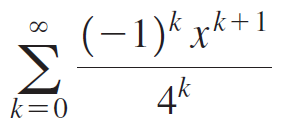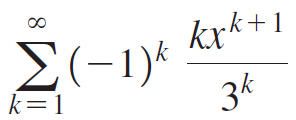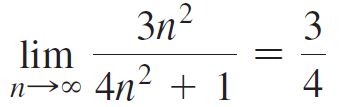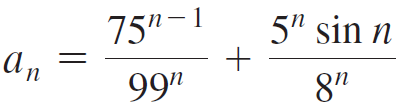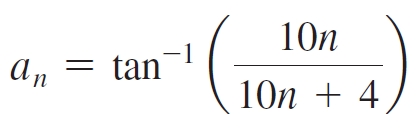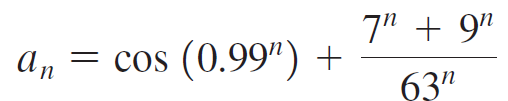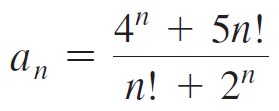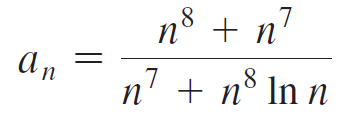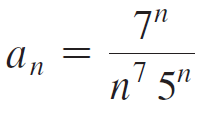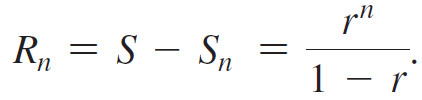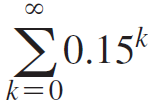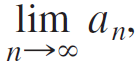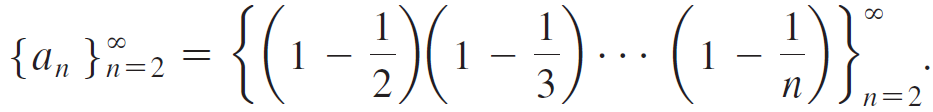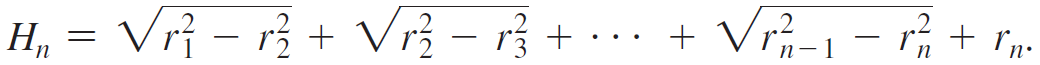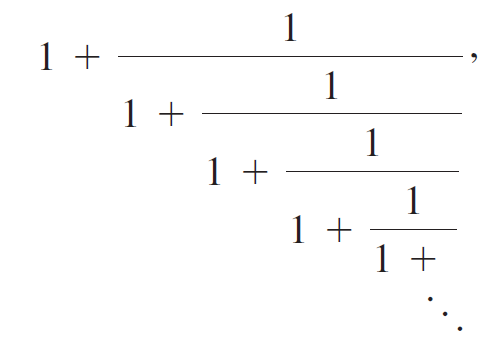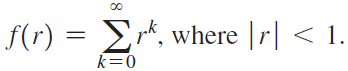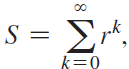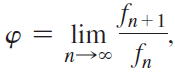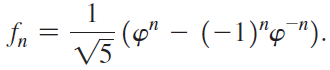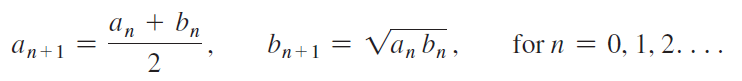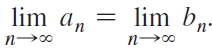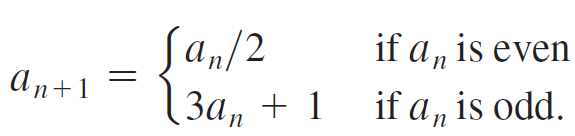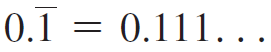Calculus Early Transcendentals 2nd edition William L. Briggs, Lyle Cochran, Bernard Gillett - Solutions
Unlock a comprehensive understanding of calculus with our meticulously crafted solutions to "Calculus Early Transcendentals 2nd edition" by William L. Briggs, Lyle Cochran, and Bernard Gillett. Access our online answers key for precise solutions and explore the solution manual available in PDF format for detailed insights. Dive into solved problems, questions, and answers that cater to your academic needs. Our test bank and chapter solutions provide step-by-step answers, making learning seamless. Benefit from our instructor manual and textbook resources, all available for free download to enhance your calculus journey.
![]() Buy $0 Christmas Gifts & Win a Prize
--h --m --s
Get Now
Buy $0 Christmas Gifts & Win a Prize
--h --m --s
Get Now
![]()