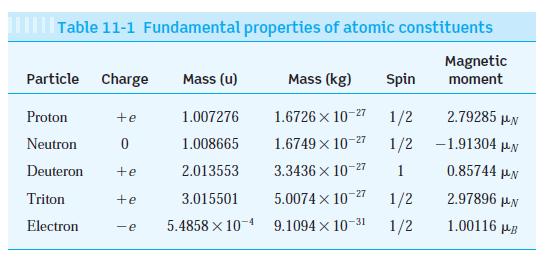
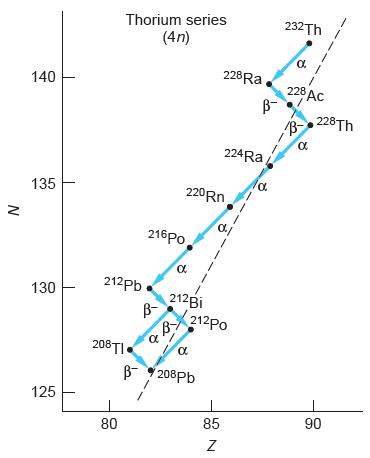
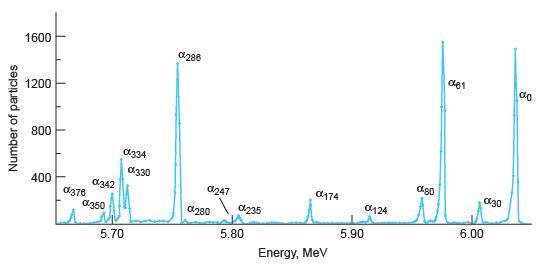
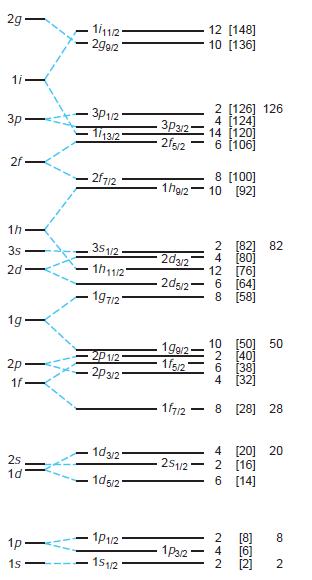
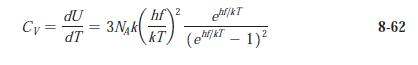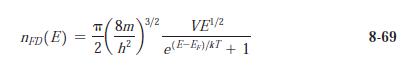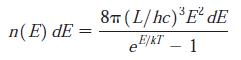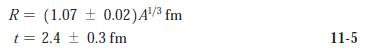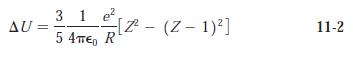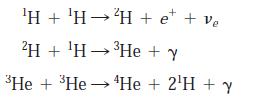Modern Physics 6th Edition Paul A. Tipler, Ralph Llewellyn - Solutions
Discover the ultimate resource for mastering Modern Physics with our comprehensive collection of questions and answers from the 6th Edition by Paul A. Tipler and Ralph Llewellyn. Access detailed solutions and step-by-step answers to enhance your understanding of each chapter. Our solution manual and instructor manual provide a wealth of solved problems, making it easier than ever to grasp complex concepts. Whether you're searching for a test bank or chapter solutions, our textbook answers key is your go-to guide. Find solutions in a convenient PDF format, available for free download, offering unparalleled support for your physics journey.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()