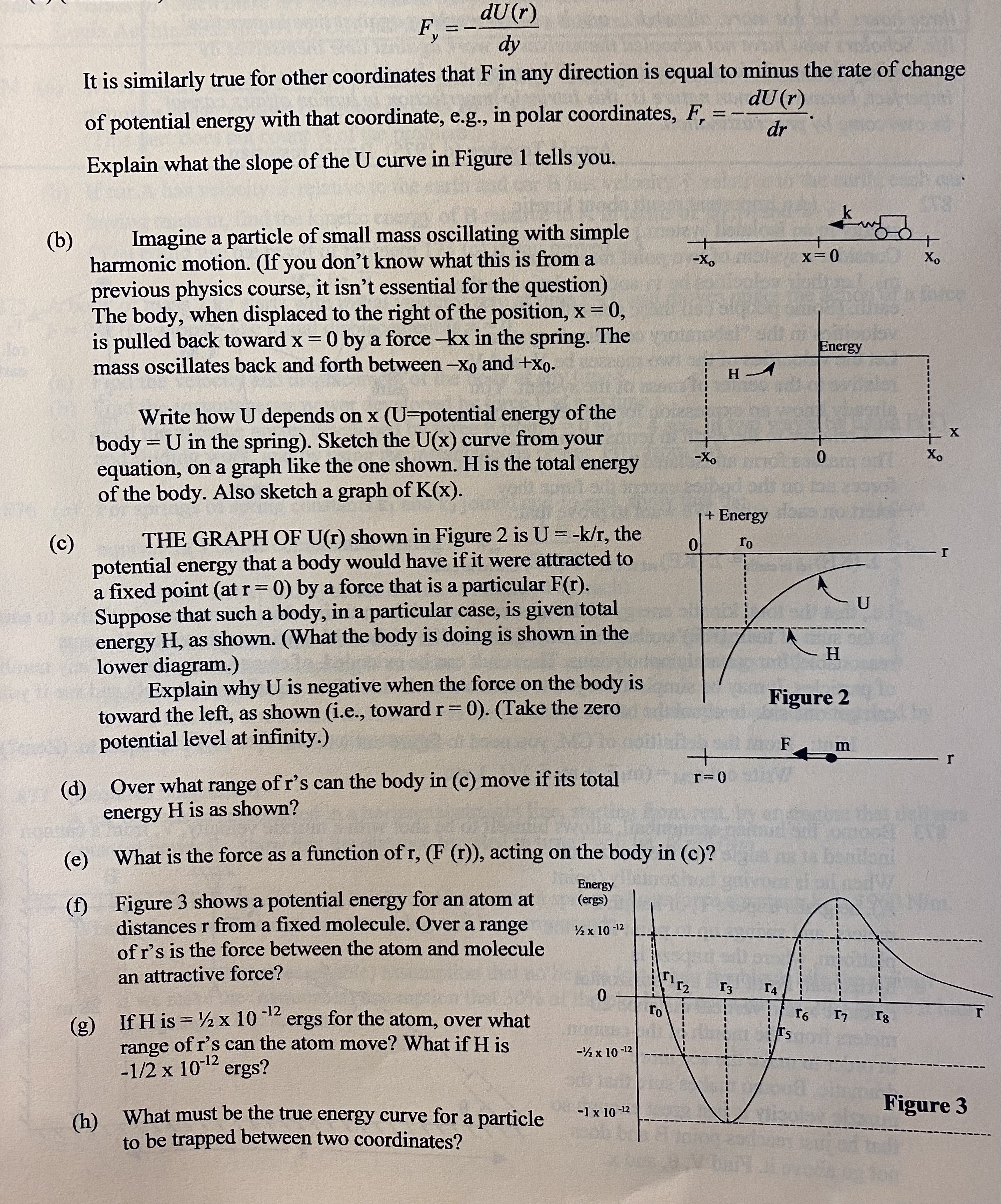
871 Introductory material. When particle or body B exerts some kind of force (e.g., gravitational, magnetic, nuclear) on a particle A, we say that B creates a field around itself and that A feels a force because A is acted on by B's field. The earth (B), for example, creates a field around itself, and any body, A, has a weight because it is in earth's gravitational field. In general, particle A, having a force on it caused by B's field, will have a potential energy, U, caused by the fact that work has to be done to move A because of the force B's field exerts on A. Usually, U will be a function of A's position, like U(x) or U(y). (If there were no field, then there would be no force on A, and it would require no work to move A around, and A would therefore have no more potential energy in one position than it would in another position; then A's potential energy would not be a function of position, but would just be a constant, or zero.) In much of the work of nuclear physics, electromagnetic theory, quantum mechanics, and molecular chemistry, it is not possible to work out exactly the total force on a particle, nor to predict its motion from Newton's Laws; for problems of this kind, energy diagrams are widely used to discuss the behavior of the particle in the field.871 (continued) Consider, for example, a trivially simple case: a particle of mass m in the earth's gravitational field near the earth's surface. We let H represent the total energy that such a particle has (or can have), and we let U(y) represent the gravitational potential energy of the particle, which varies with its vertical coordinate, y, from some reference point. We let K represent the kinetic energy of the particle, at any height y. The gravitational field (like many other kinds of fields) is a conservative field, one in which there is no friction and in which total energy is therefore conserved. Therefore K + U stays constant, and is equal to H, as Energy Figure 1 the body moves to different heights. What will an energy H graph look like for this simple case? See figure 1, which shows the energy plotted vertically against the height, y, - K plotted horizontally. The total energy, H, is a constant for all values of y. the potential energy U(y) = mgy, varies linearly with y from zero energy level to up to its maximum value, U = H. K is a graph, as shown, equal to H - U. An important point to notice about such graphs is that the U and H curves (K is usually not plotted, to avoid cluttering the U(y) = mgy graph.) determine the range of coordinates over which the y particle can move. In figure 1, we see immediately that y y max cannot be greater than ymax, where U = H. The reason is as follows. K (=1/2 mv ) must always be positive at all positions. Also, K = H- U. Therefore, H - U must always be positive, or, in other words, U cannot ever be greater than H. If H is +10, U can be anything from - co to +10, but nothing greater than +10. If H is -15, U can be anything from -co to -15, but not greater than -15. Therefore, when we look at Figure 1, we see immediately that the upper limit of possible y values is ymax where U = H, since U cannot be greater than H. This graph corresponds to throwing a body upward from the y = 0 position with a certain initial kinetic energy, K - H. It then goes upward to a maximum height ymax, where U = H. We also need to say something about the potential energy, U(y), and the force exerted on the particle by the field at coordinate y. Consider again the simple case above of a particle in the earth's gravitational field neat the earth's surface. Suppose that you exert a force upward on the body equal and opposite to its weight, so that the body can move up or down at constant velocity. The increase in its potential A F that you exert on m energy (when you raise it against the gravitational force exerted on it by the earth) is found from Myiono Inithoton s VF that field exerts on m dU = work you do in rising mass a height dy = (F you exert) (dy) Earth = (-F the field exerts) (dy). The problem begins here. (a) Continue the reasoning directly above, and show that if Fy is the Y force exerted on the particle by the field, and U(y) is the potential energy of the particle in the field at any height y, thenF, = du (r) dy It is similarly true for other coordinates that F in any direction is equal to minus the rate of change of potential energy with that coordinate, e.g., in polar coordinates, F, = du(r) dr Explain what the slope of the U curve in Figure 1 tells you. (b) Imagine a particle of small mass oscillating with simple harmonic motion. (If you don't know what this is from a -x. X =0 Xo previous physics course, it isn't essential for the question) The body, when displaced to the right of the position, x = 0, is pulled back toward x = 0 by a force -kx in the spring. The Energy mass oscillates back and forth between -Xo and +xo- H - Write how U depends on x (U-potential energy of the body = U in the spring). Sketch the U(x) curve from your X equation, on a graph like the one shown. H is the total energy -Xo of the body. Also sketch a graph of K(x). + Energy (c) THE GRAPH OF U(r) shown in Figure 2 is U = -k/r, the To potential energy that a body would have if it were attracted to a fixed point (at r = 0) by a force that is a particular F(r). Suppose that such a body, in a particular case, is given total energy H, as shown. (What the body is doing is shown in the lower diagram.) H Explain why U is negative when the force on the body is toward the left, as shown (i.e., toward r = 0). (Take the zero Figure 2 potential level at infinity.) Fam (d) Over what range of r's can the body in (c) move if its total r = 0 energy H is as shown? (e) What is the force as a function of r, (F (r)), acting on the body in (c)? ( f ) Energy Figure 3 shows a potential energy for an atom at (ergs) distances r from a fixed molecule. Over a range 1/2 x 10 -12 of r's is the force between the atom and molecule an attractive force? 13 14 (g) If H is = 1/2 x 10 4 ergs for the atom, over what To range of r's can the atom move? What if H is -1/2 x 10-12 ergs? -1/2 x 10 -12 (h) What must be the true energy curve for a particle -1 x 10 -12 Figure 3 to be trapped between two coordinates