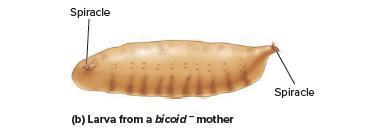
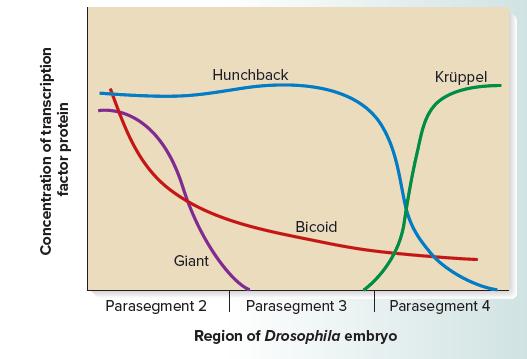
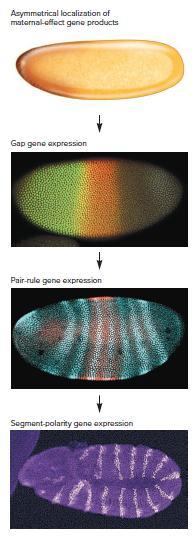
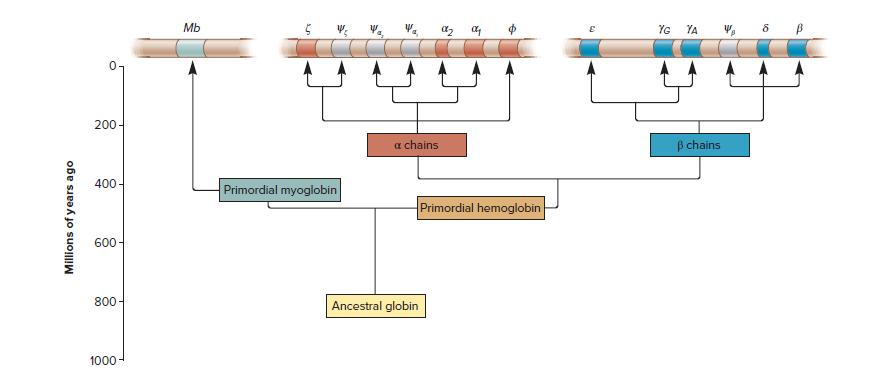
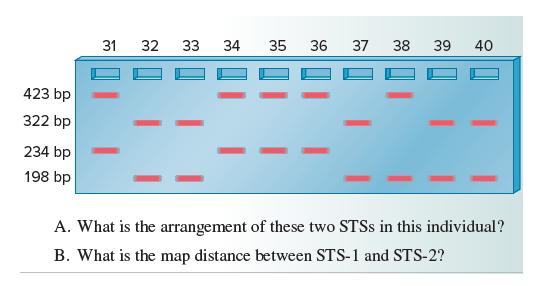
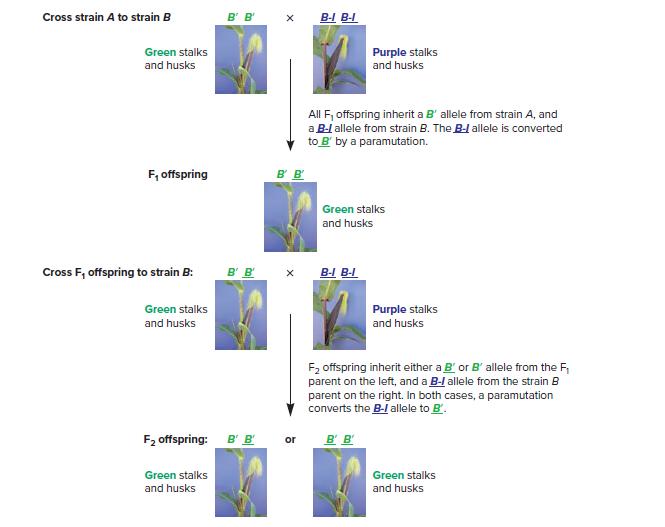
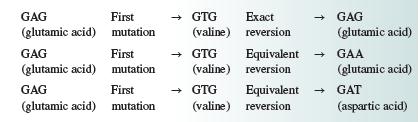
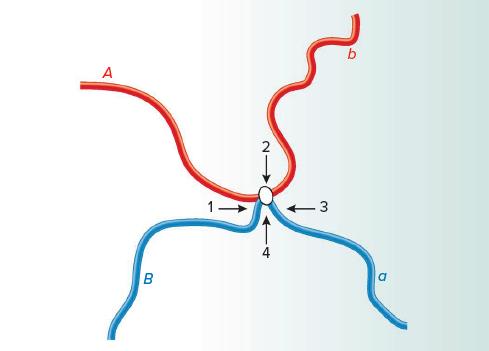
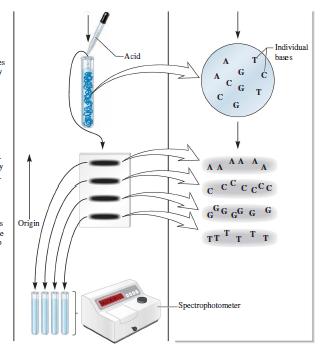
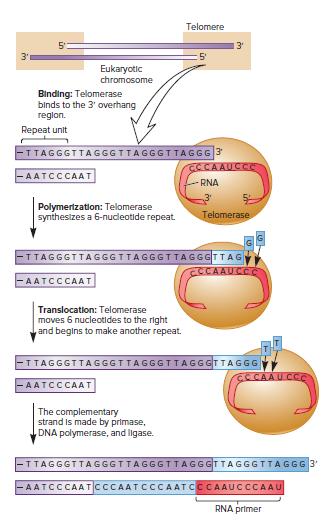
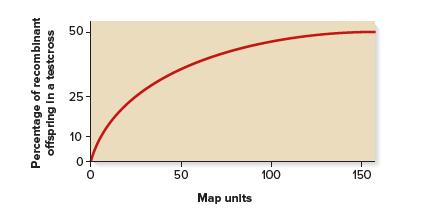
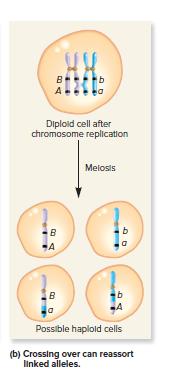
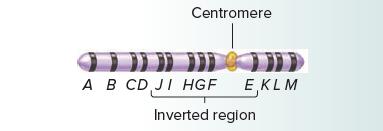
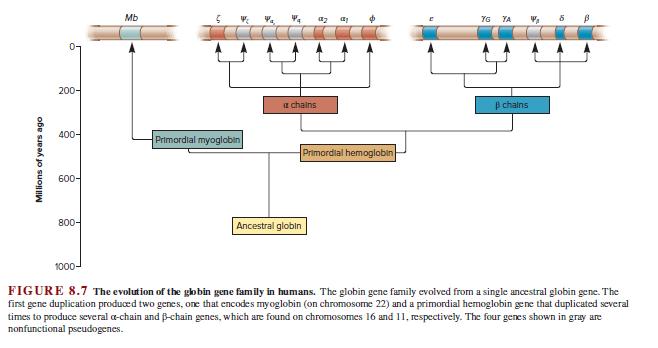
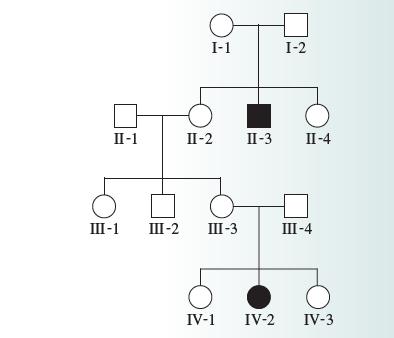
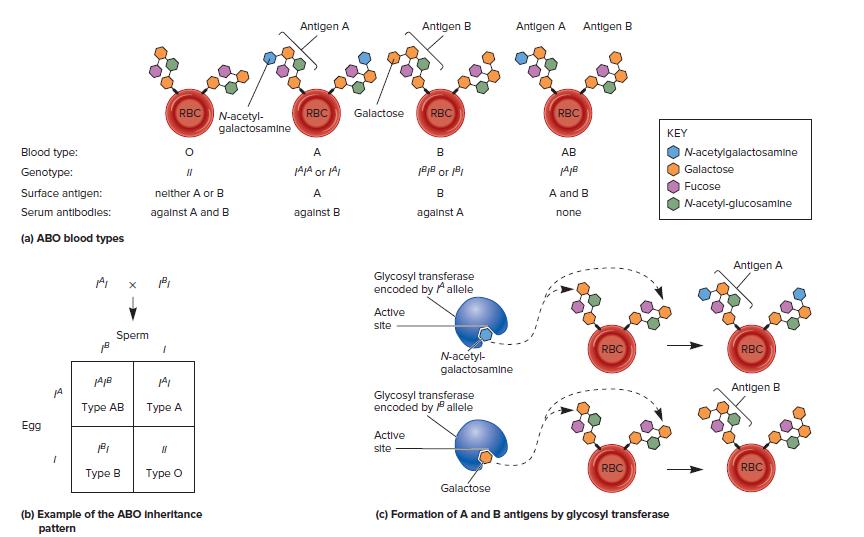
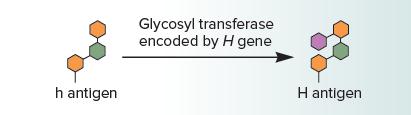Genetics Analysis And Principles 7th Edition Robert Brooker - Solutions

Discover the ultimate resource for mastering "Genetics Analysis And Principles 7th Edition" by Robert Brooker. Dive into a comprehensive collection of solved problems, answers, and solutions available online. Access the answers key to enhance your understanding with step by step answers for all chapter solutions. Utilize the solution manual, textbook, and instructor manual to guide your learning. Explore questions and answers with our test bank, ensuring you're well-prepared for any assessment. Enjoy the convenience of solutions in a downloadable PDF format, available for free download. Unlock the secrets to genetic analysis with ease and confidence.