A sinusoidally varying driving force is applied to a damped harmonic oscillator.

(a) What are the units of the damping constant b?

(b) Show that the quantity ˆškm has the same units as b.

(c) In terms of F_max and k, what is the amplitude for ω_d = ˆšk/m when (i) b = 0.2 ˆškm and (ii) b = 0.4 ˆškm? Compare your results to Fig. 14.28.

Figure 14.28:

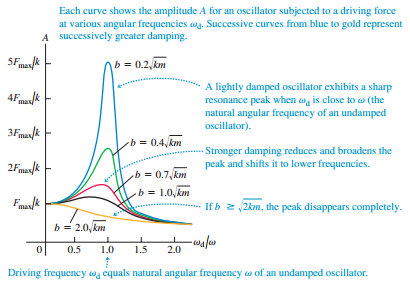
Each curve shows the amplitude A for an oscillator subjected to a driving force at various angular frequencies wg. Sucessive curves from blue to gold represent A successively greater damping. 5Fmak b = 0.2, km A lightly damped oscillator exhibits a sharp resonance peak when w, is close to w (the natural angular frequency of an undamped oscillator). 4Fmk F b = 0.4,km Stronger damping reduces and broadens the peak and shifts it to lower frequencies. 2Fiman/k b = 0.7, km b = 1.0,km Fma/k --. If b z 2km, the peak disappears completely. b = 2.0,km 0.5 1.0 1.5 2.0 Driving frequency wg equals natural angular frequency w of an undamped oscillator.