Question: A dynamic model of a continuous-flow, biological chemostat has the form where X is the biomass concentration, S is the substrate concentration, and C is

A dynamic model of a continuous-flow, biological chemostat has the form where X is the biomass concentration, S is the substrate concentration, and C is a metabolic intermediate concentration. The dilution rate, D, is an independent variable, which is defined to be the flow rate divided by the chemostat volume.Determine the value of D, which maximizes the steady-state production rate of biomass, f, given byf =DX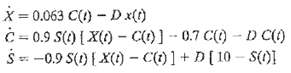 X = 0.063 C() - D x() C = 0.9 S(t) [

X = 0.063 C() - D x() C = 0.9 S(t) [ X()- C)]- 0.7 C()- D C() -0.9 S(1) | X(1) C(1) ]+ D[ 10 - S(1)I

Step by Step Solution

★★★★★

3.36 Rating (183 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Assuming steady state behavior ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

38-E-C-E-P-C (323).docx

120 KBs Word File

Students Have Also Explored These Related Chemical Engineering Questions!

The Helmholtz function of a substance has the form

The moving average model of order q has the form where et is a serially uncorrelated random variable with mean 0 and variance 2e. a. Show that E(Yt) = 0. b. Show that the variance of Yt is c. Show...

A dynamic model of the stirred-tank heating system in Fig was derived in Chapter 6. Use this model to do the following: (a) Derive an expression for the relative gain array. (b) Design art ideal...

Refer to Section 2.4.9 given in the course text on pages 31-33. This example refers to the results given in Figure 2.14 that were produced by solving the model eqs. 2-98 to 2-101 using a numerical...

a) In a batch cultivation of a microorganism, the following data has been obtained. The unit for X is g/L. Calculate the maximus specific growth rate ( -max) b) The same microorganism is used in a...

Question 1 45 Marks A group of chemical and biochemical engineers is considering the design of a control system to control the biomass production from a bioreactor. Figure 1 provides the schematic...

Need a matlab code for this assignment. thank you Consider a biochemical reactor where biomass and a desired product are produced by microbial growth from a single, rate limiting substrate. Denote...

In this problem, we will analyze a dynamic model of the two-species CSTR bioreactor shown in Fig. 5.24. On the left, fresh media with a substrate concentration Sin enters at a volumetric flow rate Q....

Q8 (20 pts) The Monod equation is a mathematical model for the growth of microorganisms. It is named for Jacques Monod who proposed using an equation of this form to relate microbial growth rates in...

Chapter 7: Wastewater Management IN THIS CHAPTER U.S. wastewater regulations Sources of contamination of wastewaters Classification of water pollutants Characteristics of wastewater Wastewater...

During 2014, Ortega Corporation had net income of $82,000. Included on its income statement were depreciation expense of $4,600 and amortization expense of $600. During the year, Accounts Receivable...

A scientist has devised a new method of isolating individual particles. He claims that this method enables him to detect simultaneously the position of a particle along an axis with a standard...

Question 2 . 3 ( Total: 5 4 marks ) Ace - It Racquets Inc. is a public company that manufactures and sells tennis racquets. The company has expanded internationally, and its auditors have resigned...

Problem 12-53 (Algo) Dual and Single Allocation Rates (LO 12-6) Burwell Manufacturing is organized into two divisions (Agriculture and Mining) and a corporate headquarters. The financial group of the...

After watching Jon Sayles's 1996 film Lone Star , answer the following five questions, utilizing relevant terminology. Answers should be concise and precise. 1. Is the film's ideology neutral,...

Powder Mountain (PM) ski resort is currently using a Skidata barcode ticketing system. PM purchased the system three years ago for $1 million. The system includes barcode scanners and point-of-sale...

The following transactions relate to the General Fund of the City of Buffalo Falls for the year ended December 31, 2020: 1. Beginning balances were: Cash, $106,000; Taxes Receivable, $209,000;...

b. In your audit of Aviary Industries for calendar year 2011, you found several matters that you believe represent possible adjustments to the company's books. These matters are described below....

The supply manager of ACME Company wants to set up a sampling plan abiding by the following conditions: AQL = 4% Supplier risk = 6% AOQL = 5% Help him finding out the most economical plan.

For the network shown, choose the values of Rin and Ro such that Vo is maximized. What is the resulting ratio, Vo / Vs? R, Rs V. R. Vin Vs

In many amplifier applications we are concerned not only with voltage gain, but also with power gain. Power gain = Ao =(power delivered to the load)/(power delivered by the input)Find the power gain...

Find the power absorbed by the 10-K ohms resistor in the circuit shown. 11 mA 10 k 2000

When you have visited edinburg, you have plan to purchase a benz car for 40000 pounds , payable in 3 months. You have enough cash at your bank in california city, which pays 0.35% interest per month,...

An investor must choose between two bonds: Bond A pays $85 annual interest and has a market value of $760. It has twelve years to maturity. Bond B pays $97 annual interest and has a market value of...

Please answer Question #39 and show work. A Treasury bill matures in 68 days and has a bond equivalent yield of 4.05 percent. What is the effective annual rate? A. 4.12 percent B. 4.14 percent C....