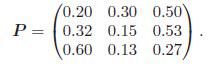
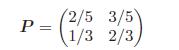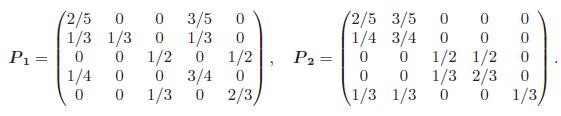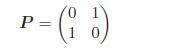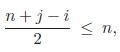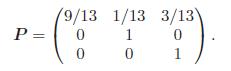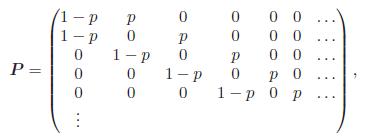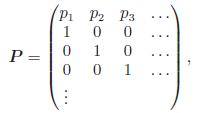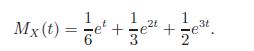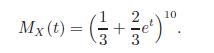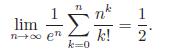Fundamentals Of Probability With Stochastic Processes 4th Edition Saeed Ghahramani - Solutions
Explore the ultimate resource for mastering "Fundamentals of Probability with Stochastic Processes," 4th Edition by Saeed Ghahramani. Our comprehensive answers key and online solutions provide in-depth insights into textbook questions and answers. Access the solution manual and solutions PDF for detailed, step-by-step answers to solved problems. Enhance your understanding with our instructor manual and test bank, offering chapter solutions that guide you through complex concepts. With free download options, you can easily access textbook resources and enjoy the convenience of having all your study materials in one place. Dive into the world of probability and stochastic processes with confidence!
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()