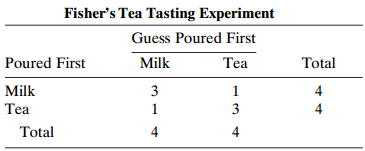
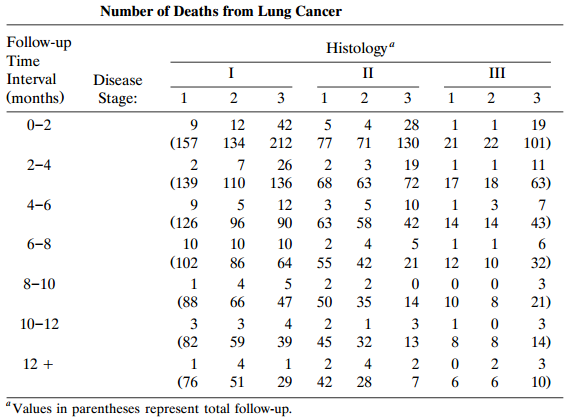
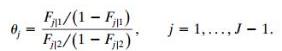![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


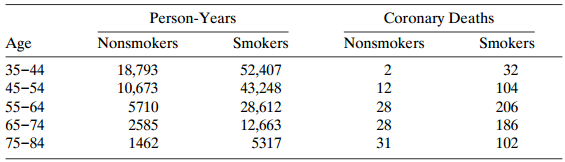

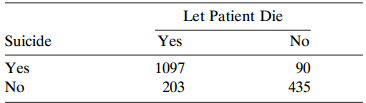
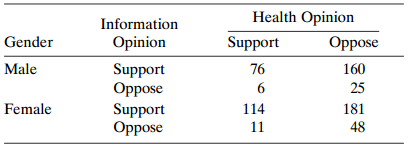
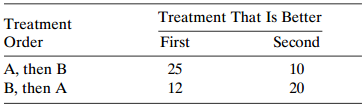
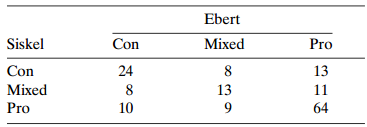
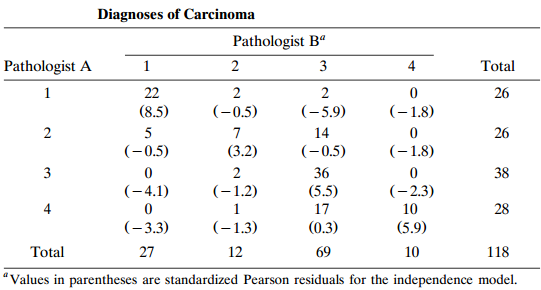
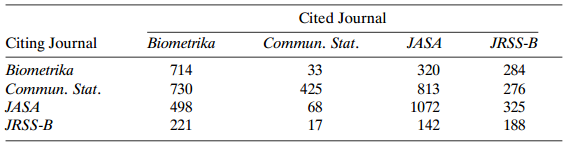
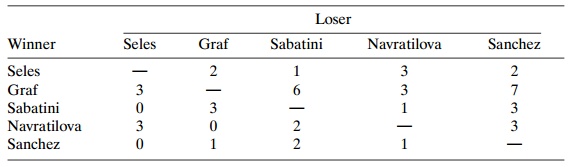
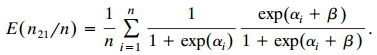
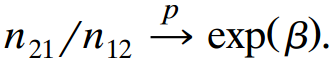
![var n (BM )] -(π, προ) + (π, π, ) < (πι, προ)+ (π.1 ρ+)7!. - + σ- ar ( β ] %3D νε](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1539/7/1/1/0745bc620621ee451539693507499.jpg)