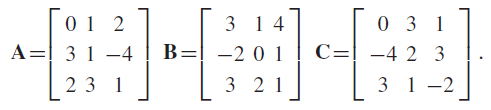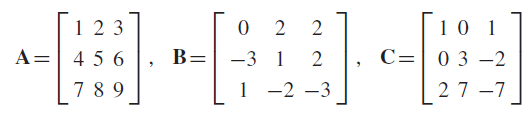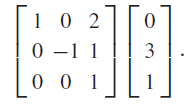Mathematics for Physical Chemistry 4th Edition Robert G. Mortimer - Solutions
Discover the ultimate resource for mastering "Mathematics for Physical Chemistry 4th Edition" by Robert G. Mortimer. Access a comprehensive collection of online answers and solution manuals, including answers key, solutions PDF, and step-by-step answers to solved problems. Enhance your understanding with our test bank and chapter solutions, meticulously crafted to assist both students and instructors. Our instructor manual and textbook solutions offer valuable insights, and the best part is, you can enjoy these resources with a free download. Unlock the secrets to success with our detailed questions and answers, tailored to support your academic journey.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()





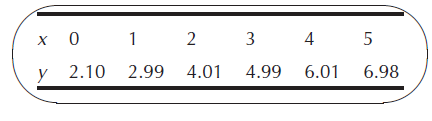




![0.76 In] = (2.00 x 10–*dl g-')) Mo](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/2/5/1/4395c29ecaf099cb1546234045387.jpg)

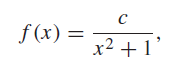
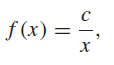

![10 X1 1-1 1 1 1 -1 1 [1 1 6. 1 х2 4 Хз -1] [ x4 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/0/9/4/1925c27867043f941546076794757.jpg)
![1 1 3 6. 1 X1 2111 5 X2 12 3 4 10 хз [7 [201 4] Lx4. ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/0/9/6/3725c278ef44238f1546078974351.jpg)

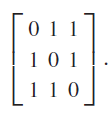
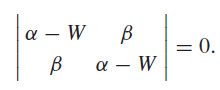
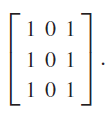
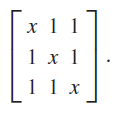
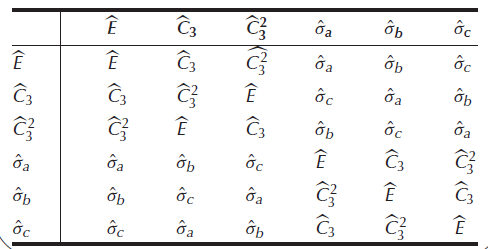
![[100 0 10 E, 001 |-1/2 -V3/2 0 V3/2 -1/2 0= A, -1/2 V3/2 0 -/3/2 –1/2 0 = B, 0 1 1/2 3/2 0] V3/2 –1/2 0 0 0 1 = C, 1/2 -V3/2 0 -/3/2 -1/2 0 = D, 0 0 1 -100 ốc 0 10 0 0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1606/9/9/6/0455fc8d04df3b3a1606996045139.jpg)