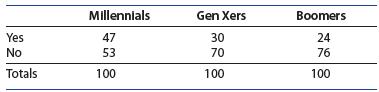
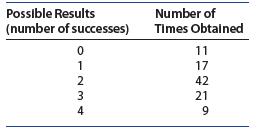
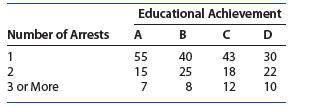
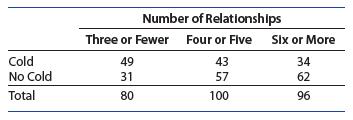
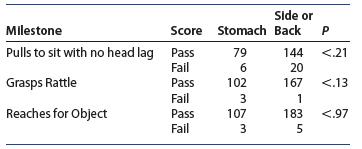
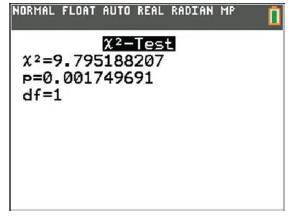
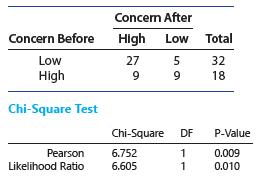
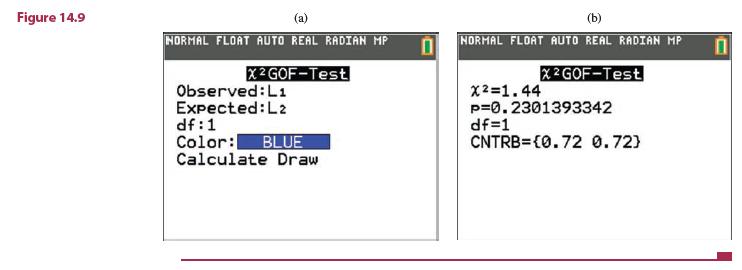
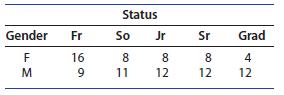
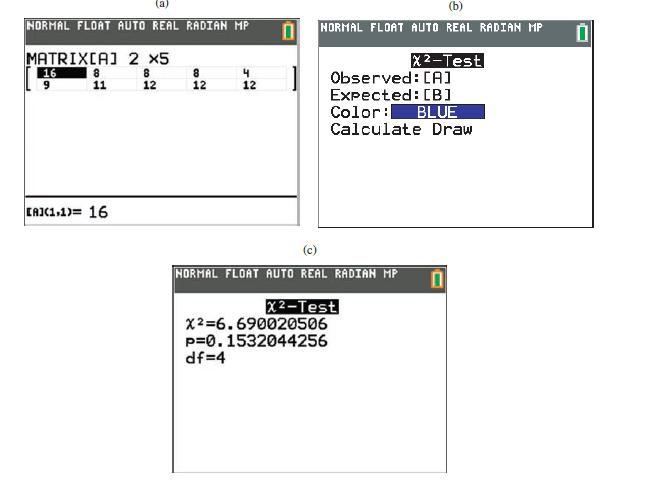
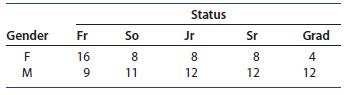
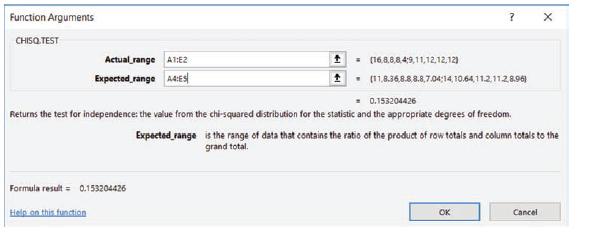
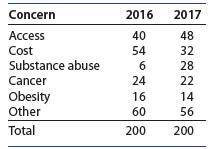
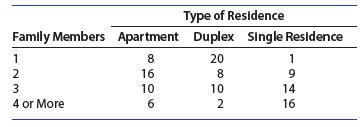
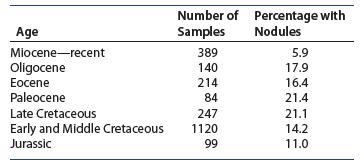
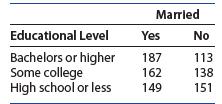
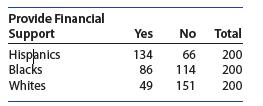
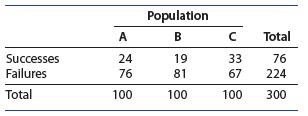
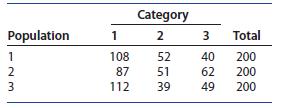
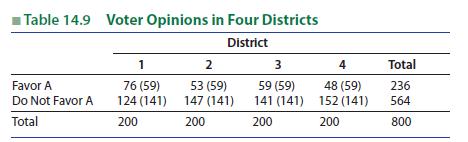
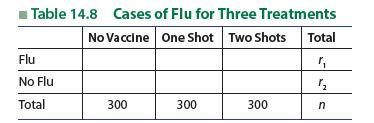
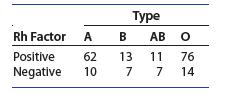
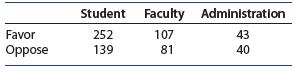
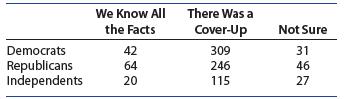
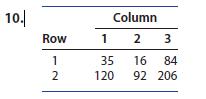
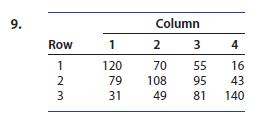
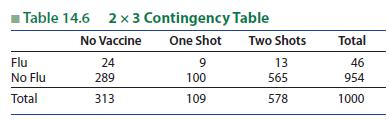
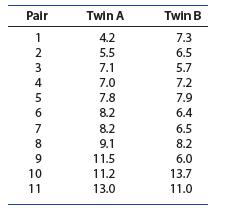
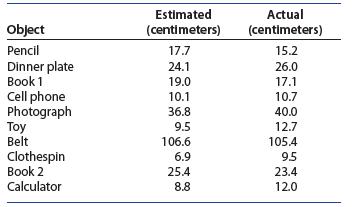
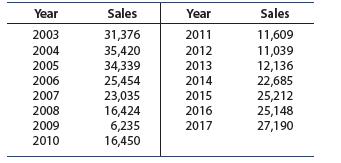
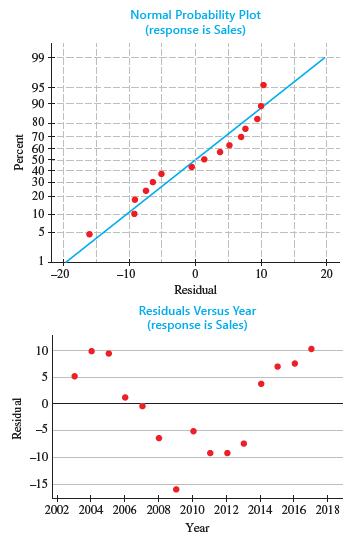
Introduction To Probability And Statistics 15th Edition William Mendenhall Iii , Robert Beaver , Barbara Beaver - Solutions
Discover comprehensive resources for "Introduction To Probability And Statistics 15th Edition" by William Mendenhall III, Robert Beaver, and Barbara Beaver. Access an extensive collection of questions and answers online, complete with a detailed answers key and solution manual. Find solutions in PDF format for solved problems, ensuring you grasp each concept with ease. Explore the test bank and chapter solutions for in-depth understanding. Our step-by-step answers guide you through each problem, while the instructor manual complements your learning. This textbook is an invaluable resource, and you can enjoy a free download of these materials for enhanced study support.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()