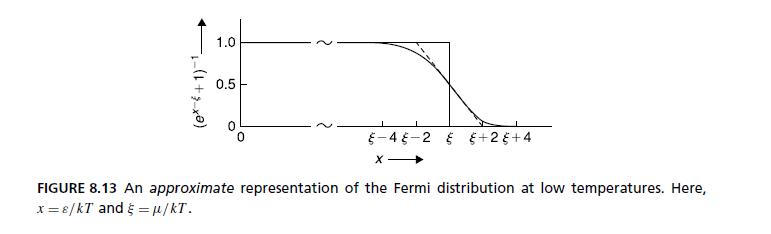
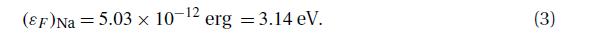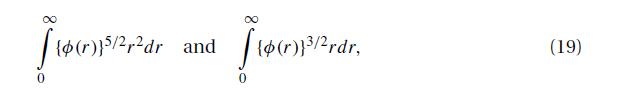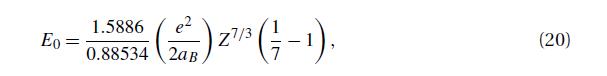Statistical Reasoning For Everyday Life 5th Edition Jeff Bennett, William Briggs, Mario Triola - Solutions

Discover the comprehensive answers and solutions for "Statistical Reasoning For Everyday Life 5th Edition" by Jeff Bennett, William Briggs, and Mario Triola. Our online platform provides a detailed answers key and solution manual, available in a convenient solutions PDF format. Explore solved problems and questions and answers tailored for students and instructors alike. Benefit from our test bank and chapter solutions, offering step-by-step answers to enhance your understanding. Whether you seek the instructor manual or the complete textbook, enjoy the ease of free download and elevate your learning experience today.