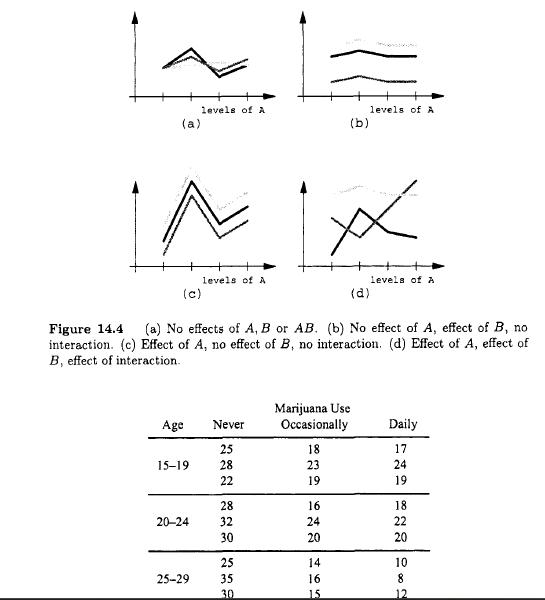
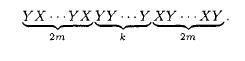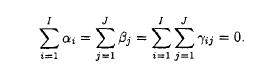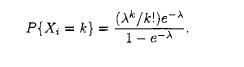Probability And Statistical Inference 2nd Edition Robert Bartoszynski, Magdalena Niewiadomska-Bugaj - Solutions
Unlock the comprehensive understanding of "Probability And Statistical Inference 2nd Edition" by Robert Bartoszynski and Magdalena Niewiadomska-Bugaj with our extensive collection of solved problems and step-by-step answers. Access the complete solutions manual and instructor manual for detailed explanations. This essential resource includes answers key, chapter solutions, and a test bank for enhanced learning. Whether you are looking for solutions PDF or seeking questions and answers for better preparation, our online platform offers a textbook companion with free download options for seamless study support.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()