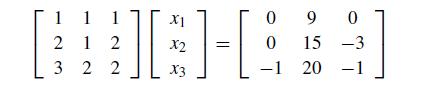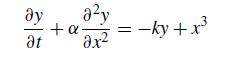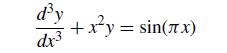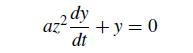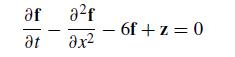Numerical Methods With Chemical Engineering Applications 1st Edition Kevin D. Dorfman, Prodromos Daoutidis - Solutions
Unlock a world of knowledge with "Numerical Methods With Chemical Engineering Applications" by Kevin D. Dorfman and Prodromos Daoutidis. Access the complete answers key and solutions manual to enhance your understanding of complex concepts. Dive into solved problems and explore step-by-step answers designed to guide you through each chapter. With the online solutions PDF, get comprehensive questions and answers, perfect for exam preparation with the test bank. Whether you're an instructor or a student, the textbook and instructor manual provide invaluable resources. Enjoy the convenience of free download options to ensure you have everything you need at your fingertips.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



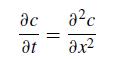
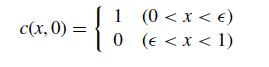
![LU . [ 1 m2,1 m3,1 0 0 1 0 1 m3,2 ][ a1.1 0 0 (1) 1.2 (2) 92,2 0 (1) 1.3 (2) 92.3 (3) a3,3 (2.11.10)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/2/066652f8122bd7a01697612065287.jpg)
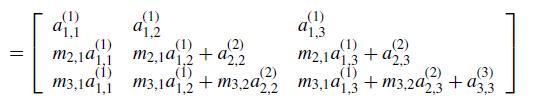
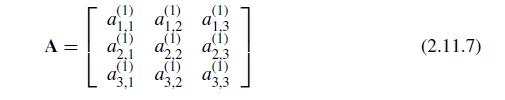
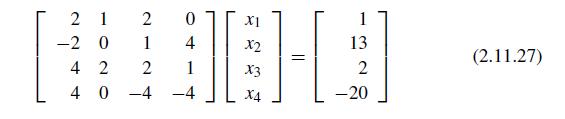

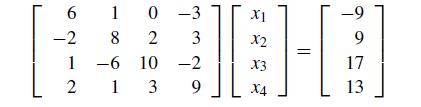
![1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 function problem2_78 clc A = [2 1 3; 4 2 1; 1 1 1]; n = 3; q = 1; for](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/5/284652f8db4015911697615280976.jpg)

![= [42] A =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/5/129652f8d1901ecf1697615126468.jpg)

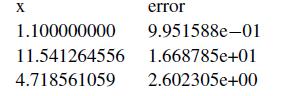
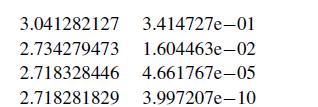


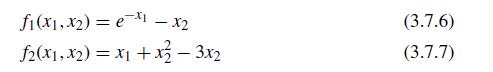
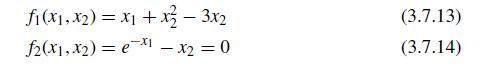
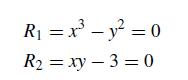
![X [4] =>](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/2/4/572652fb1fc755041697624569823.jpg)
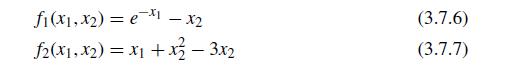
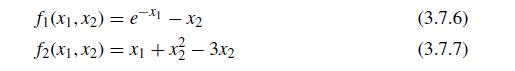
![F(x): = {]-[ fi(x) f2(x) f3(x) XX2X3x+x-1.34 X1x2-x-0.09 et ex2 + x3 -0.41 -](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/2/4/581652fb20554c3f1697624578688.jpg)
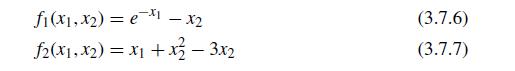
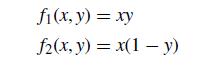
![=[] y X =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/2/4/811652fb2eb2d7831697624808402.jpg)
![(0) 2 =[] 1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/2/4/819652fb2f3ded161697624818159.jpg)






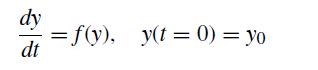




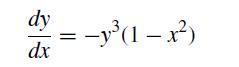


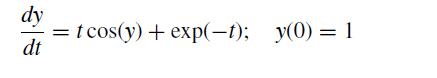




![f[x, xj, xk] = f[xi, xj] - f[xj, xk] Xi Xk (8.2.27)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/6/9876530f3ebcf1ae1697706986837.jpg)
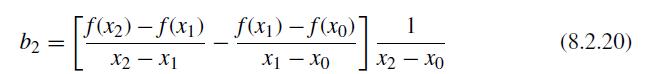

![f[xn, xn-1,...,x, xo] = = f[xn, xn-1,...,x2, X] - f[xn-1,..., X1, Xo] Xn - XO (8.2.28)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/7/0156530f4070df171697707013258.jpg)
![f[xi, xj] = f(xi) - f(xj) x - xj (8.2.26)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/7/0536530f42d8b5a61697707052218.jpg)
![f[x2, x1, xo]: = [f(x) - f(x) X2 - X1 2]: f(x)-f(xo) X1 - XO 1 X2 - XO (8.2.32)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/7/0756530f443c20bb1697707074264.jpg)
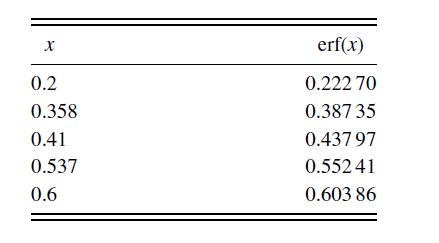
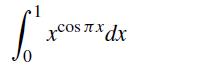

![f[X3, X2, X1, Xo] f[x3, x2, x1] - f[x2, X1, Xo] X3 - XO (8.2.33)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/7/1676530f49f0d7aa1697707165694.jpg)


![f(x) = 1 1+25x x = [-1, 1].](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/8/8206530fb145fc8b1697708818534.jpg)

![6 7 00 O 8 9 end end legend ('ytilde', 'y', 'yhat') title(['Plot for n = ', num2str (n)])](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/9/0996530fc2bd50c91697709097476.jpg)

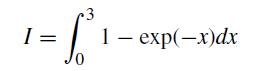
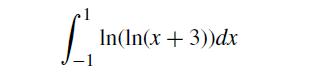
![xp [(x2)+7][x -J](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/9/3116530fcff2fd5d1697709309183.jpg)
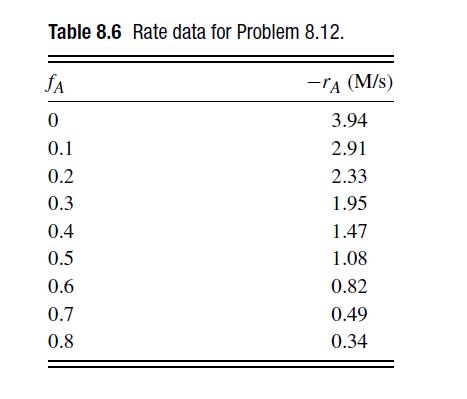

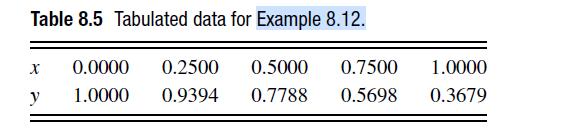
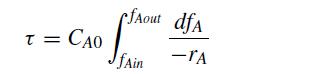
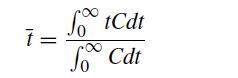
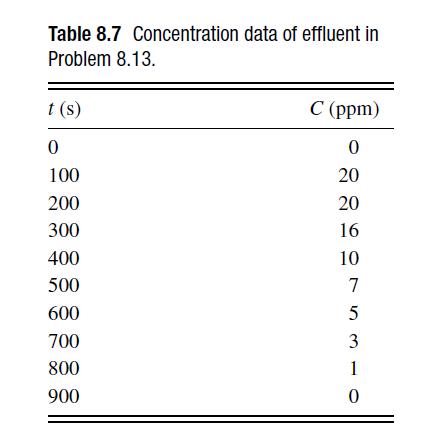
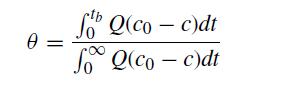
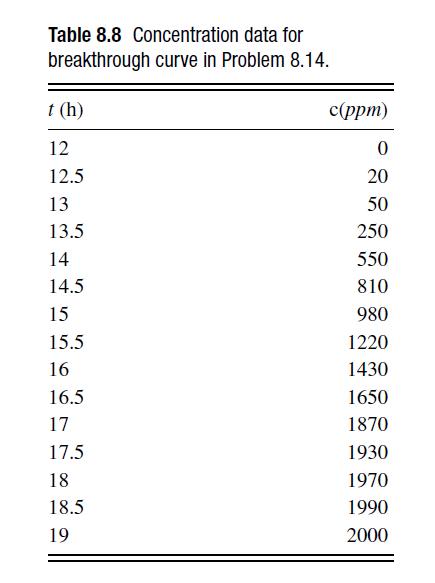
![6 12 Ld 00-[- + ) - ()]] 1/1/4/ C(z) = exp 2s Z](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/9/6846530fe74ddb5e1697709681301.jpg)
![6 12 L + [ - + ^ { ( 9 ) - ( 9 ) } ] Z C(z) = exp](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/9/7276530fe9f075d21697709725299.jpg)
![= [ [ C () - 1] dz Zi r =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/7/0/9/7966530fee44453d1697709793720.jpg)