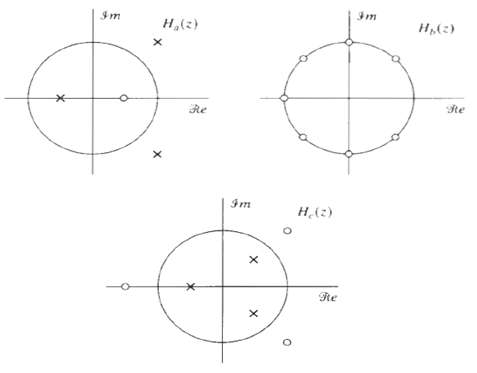
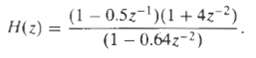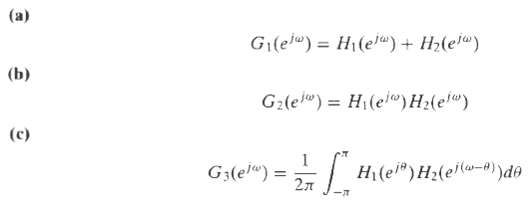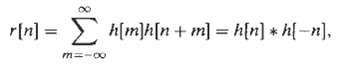![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


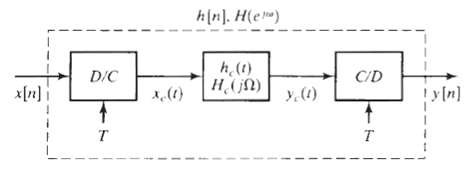
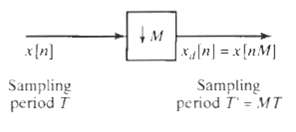

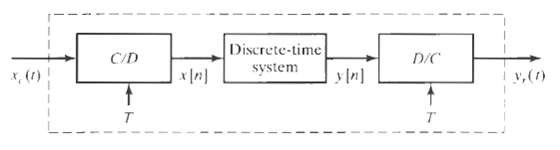
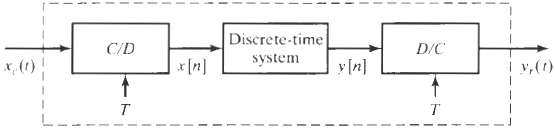
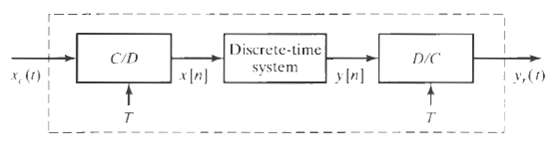
![Interpolator Decimator Lowpass filter Gain = 1 Cutoff = 1!M ä,(1)] Lowpass filter Gain = L. Cutoff = niL | x,
] x;(n}](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/6/6/9635c629e73cb1e01550013890836.jpg)
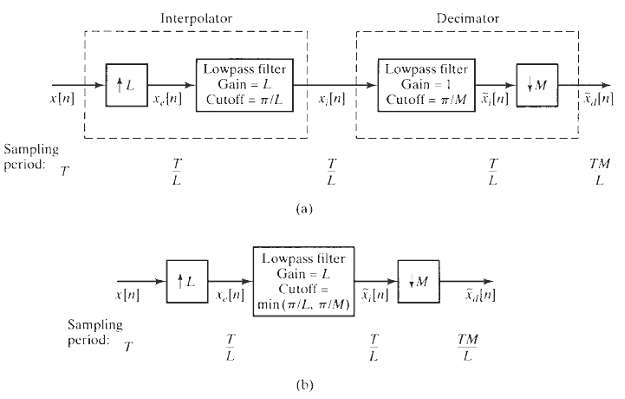


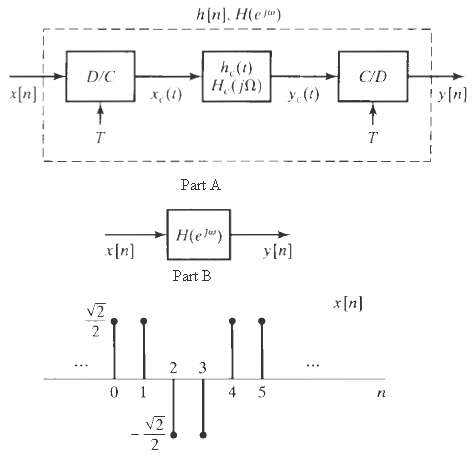




![Lowpass filter Gain = L x{n] *, [n} x, [1] Cutoff = #/L Sampling period T' = T/L Sampling period T Sampling period T' =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/7/5/7735c62c0dd2d1531550022698612.jpg)

![| S,(jN) -2п . 4000 2т 4000 0(гаd/s) | sy[n] Не) s[n] м [4]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/7/6/2425c62c2b2953fb1550023169301.jpg)


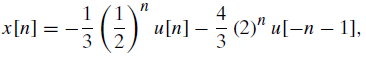
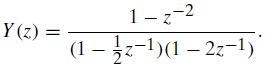


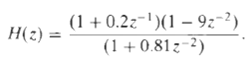

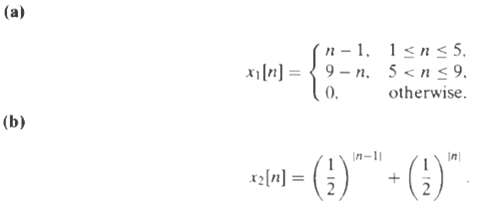
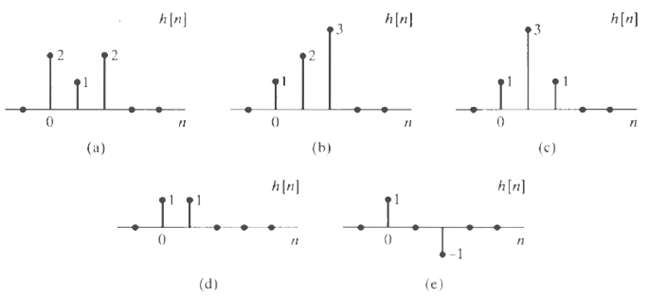
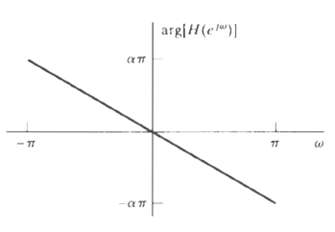
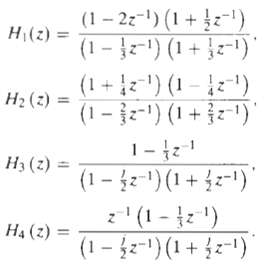
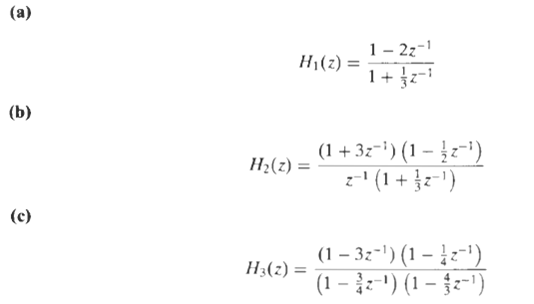
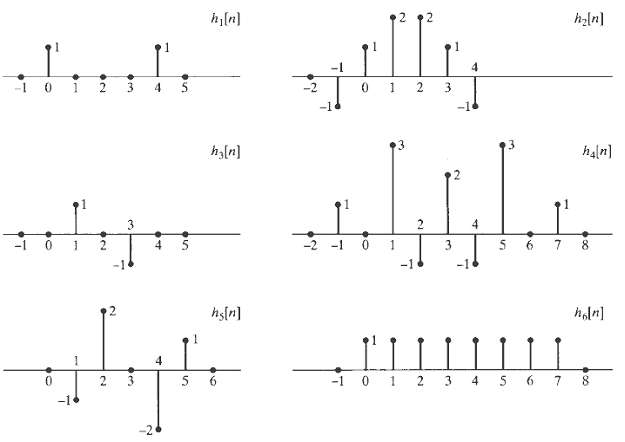
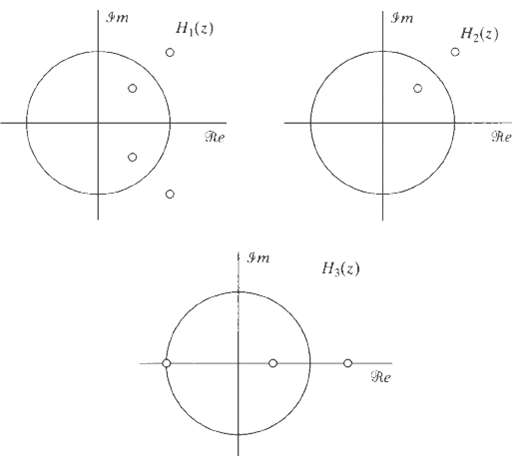
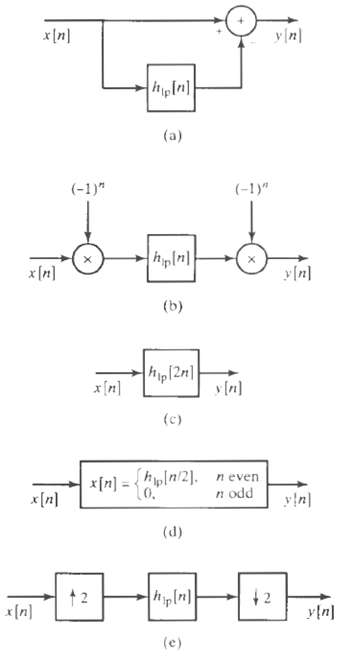
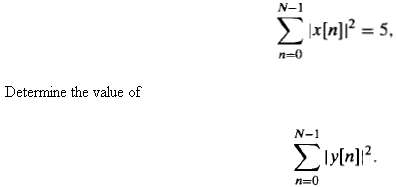
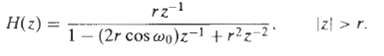


![24 y[n] = w[2n] H(z) w [n] x[n] Im Unit Mth-order pole at z = 0, M2 2 and M is an integer circle z-plane Re 2 24 G(2) x[](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/3/0/7985c651e6e0d8381550130796770.jpg)
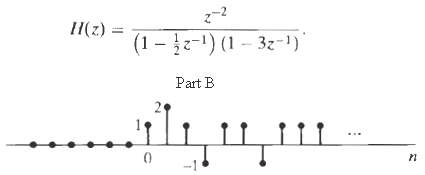
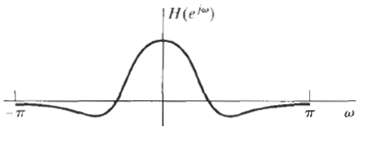


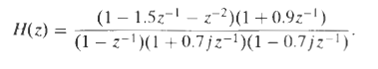
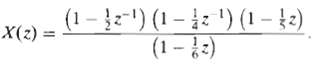
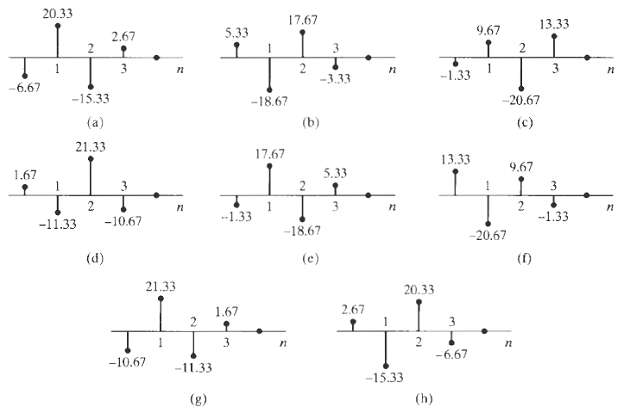
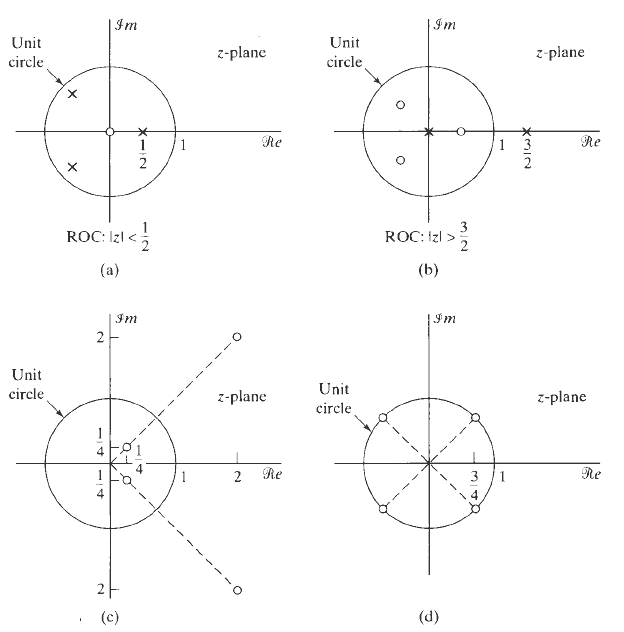
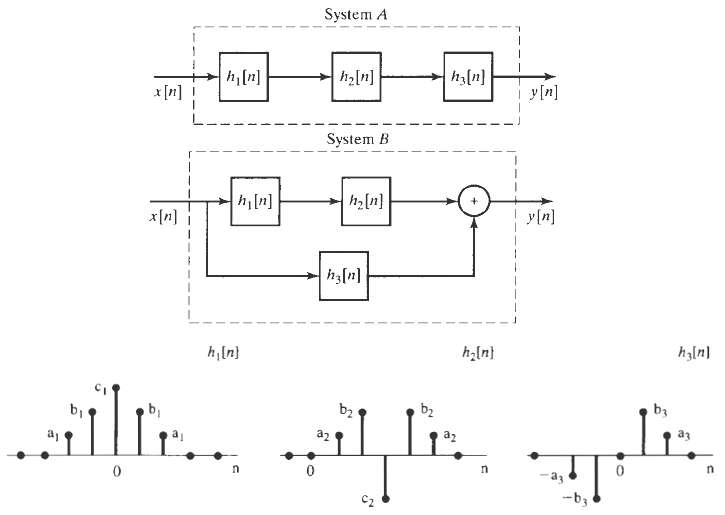

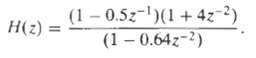
![x[n] = 5 the corresponding output is sin(0.4n) лп + 10 cos(0.57n). sin[0.3л (n - 10)1 л (п — 10) y[n] = 10](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/1/3/3/1545c6527a2370b71550133153742.jpg)